Estadística d’una variable
Nivell educatiu: 3r d’ESO
Paraules clau: estadística, qualitativa, quantitativa, discreta, contínua, GeoGebra
Resum
Aquest tema d’estadística descriptiva està orientat a l’ensenyament secundari. Normalment hi ha molta confusió entre les propietats estadístiques, quines es podem utilitzar en cada model estadístic. Per això el fil conductor del tema són els models estadístics.
Índex
- Resum
- Introducció
- El model estadístic qualitatiu
- El model estadístic quantitatiu discret
- El model estadístic quantitatiu continu
Introducció
L’estadística és la ciència matemàtica encarregada de recopilar, ordenar, representar i analitzar conjunts amb una gran quantitat de dades. És el coneixement matemàtic més utilitzat per les altres ciències, també en l’economia i sobre tot en la premsa.
Podeu distingir entre l’estadística descriptiva, amb la funció de conèixer els conjunts de dades i l’estadística inferencial o inductiva, que estudia el comportament dels conjunts de dades.
Les primeres estadístiques es van aplicar a la població humana i per això hi ha un vocabulari estadístic molt relacionat amb la sociologia.
La població estadística és el conjunt estudiat i és fonamental que estiga perfectament definida. La lletra ![]() majúscula s’utilitza per a indicar la grandària de la població.
majúscula s’utilitza per a indicar la grandària de la població.
L’individu és un element del conjunt i és molt important que els criteris que defineixen les estadístiques determinen sense error, si un individu pertany o no a la població estudiada.
La mostra és un subconjunt de la població, molt utilitzada quan s’estudien conjunts molt grans, per a simplificar i abaratir els costos econòmics dels estudis estadístics. La mostra ha de ser representativa de la població per minimitzar els errors produïts en l’estudi de la població. La lletra ![]() minúscula s’utilitza per a indicar la grandària de la mostra. Normalment les fórmules utilitzen la
minúscula s’utilitza per a indicar la grandària de la mostra. Normalment les fórmules utilitzen la ![]() minúscula, però si estudieu una població completa podeu substituir-la per la
minúscula, però si estudieu una població completa podeu substituir-la per la ![]() majúscula.
majúscula.
La variable estadística és la propietat estudiada i ha de ser mesurable en tots els individus que formen la població.
Per a realitzar una estadística necessitem una població i el valor de la variable de cada individu. Existeixen molts models estadístics per al tractament de la informació, en aquest curs ens centrarem solament en l’estadística descriptiva amb tres models. El model qualitatiu que utilitzareu per a variables qualitatives amb valors expressats amb paraules, el model quantitatiu discret per a variables que poden expressar-se amb nombres naturals o enters i el model quantitatiu continu per a variables que necessiten els nombres racionals o reals. No oblideu mai que les variables quantitatives tenen unitats i moltes de les característiques estadístiques que estudiareu també les tenen.
Exemples d’estadístiques qualitatives serien: la intenció de vot, la marca del mòbil, la satisfacció en un servei, les notes literals dels alumnes…
Exemples d’estadístiques quantitatives discretes serien: quantitat de fills d’una família, quantitat d’aparells electrònics que tenen les persones, quantitat d’aparells defectuosos en processos de fabricació…
Exemples d’estadístiques quantitatives contínues serien: Estudi de l’edat, de l’altura, del sou…
Les taules són les estructures principals d’ordenació de la informació, faciliten el càlcul i l’anàlisi estadístic. Penseu que les dues estructures més importants del la informació digital tenen forma de taula: els fulls de càlcul i les bases de dades.
Els models estadístics comparteixen algunes propietats i solament s’expliquen la primera vegada que apareixen. Ara estudiareu els tres models estadístics amb el mateix exemple analitzat de tres formes diferents.
Les notes escolars al llarg de la història passen per diferents models: les paraules insuficient, suficient, bé, notable, excel·lent que podeu analitzar qualitativament, els nombres 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 que podeu analitzar quantitativament de forma discreta i els nombres decimals que apareixen en els exàmens que podeu analitzar quantitativament de forma contínua.
El model estadístic qualitatiu
La taula
Aquest és el model més senzill i els valors de la variable estan definits amb paraules, poden ser nominals si no tenen ordre i ordinals si tenen ordre, però el seu tractament matemàtic és idèntic.
La intenció de vot i la marca de mòbil són variables nominals, i la satisfacció (ninguna, poca, molta, moltíssima) i les notes (insuficient, suficient, bé, notable, excel·lent) són ordinals.
Per analitzar la taula d’aquest model estadístic observareu l’exemple següent.
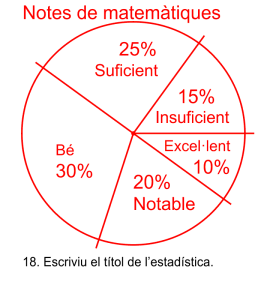
Les notes de matemàtiques dels 500 alumnes de l’institut.
| Insuficient | 75 | 0.15 | 15 | 54 | 54 |
| Suficient | 125 | 0.25 | 25 | 90 | 144 |
| Bé | 150 | 0.30 | 30 | 108 | 252 |
| Notable | 100 | 0.20 | 20 | 72 | 324 |
| Excel·lent | 50 | 0.10 | 10 | 36 | 360 |
| 500 | 1.00 | 100 | 360 |
![]() . La primera columna conté els valors que pot prendre la variable estadística. El subíndex indica la línia on està situada la informació:
. La primera columna conté els valors que pot prendre la variable estadística. El subíndex indica la línia on està situada la informació: ![]() és insuficient,
és insuficient, ![]() és suficient,
és suficient, ![]() és bé,
és bé, ![]() és notable i
és notable i ![]() és excel·lent.
és excel·lent.
![]() . La segona columna conté les freqüències absolutes. Comptabilitza la quantitat d’individus que tenen la variable amb el mateix valor. També tenen subíndex,
. La segona columna conté les freqüències absolutes. Comptabilitza la quantitat d’individus que tenen la variable amb el mateix valor. També tenen subíndex, ![]() ,
, ![]() ,
, ![]() ,
, ![]() i
i ![]() . Aquesta columna i l’anterior representen el punt de partida del càlcul de la taula. Baix de la columna està la grandària de la mostra, que és la suma de totes les freqüències absolutes
. Aquesta columna i l’anterior representen el punt de partida del càlcul de la taula. Baix de la columna està la grandària de la mostra, que és la suma de totes les freqüències absolutes ![]() . Aquesta suma es representa amb la lletra grega sigma majúscula, com cada estadística té una quantitat de línies diferents la fórmula general s’escriu de la forma
. Aquesta suma es representa amb la lletra grega sigma majúscula, com cada estadística té una quantitat de línies diferents la fórmula general s’escriu de la forma ![]() , i es lleig “La població és el sumatori de totes les freqüències absolutes”.
, i es lleig “La població és el sumatori de totes les freqüències absolutes”.
![]() . La tercera columna conté les freqüències relatives, redueix tota l’estadística a la unitat, i és calcula dividint la freqüència absoluta de cada línea entre la quantitat de mostra. Evidentment també tenen subíndexs,
. La tercera columna conté les freqüències relatives, redueix tota l’estadística a la unitat, i és calcula dividint la freqüència absoluta de cada línea entre la quantitat de mostra. Evidentment també tenen subíndexs, ![]() ,
, ![]() ,
, ![]() . El sumatori de les freqüències relatives és la unitat
. El sumatori de les freqüències relatives és la unitat ![]() i permet verificar que els càlculs són correctes.
i permet verificar que els càlculs són correctes.
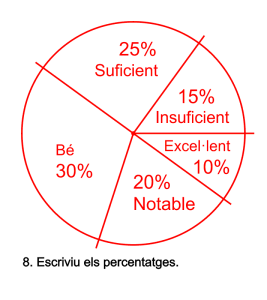
![]() . La quarta columna conté les freqüències relatives expressades en percentatge i es calcula multiplicant per
. La quarta columna conté les freqüències relatives expressades en percentatge i es calcula multiplicant per ![]() les freqüències relatives. La columna ha de sumar cent,
les freqüències relatives. La columna ha de sumar cent, ![]() . Aquesta columna és de les més importants, la més utilitzada en els informes estadístics, si mireu els articles periodístics observareu que estan farcits de percentatges.
. Aquesta columna és de les més importants, la més utilitzada en els informes estadístics, si mireu els articles periodístics observareu que estan farcits de percentatges.
![]() . La cinquena columna conté els angles dels sectors que representen cada informació en el diagrama de sectors. Es calcula multiplicant la columna de les freqüències relatives per
. La cinquena columna conté els angles dels sectors que representen cada informació en el diagrama de sectors. Es calcula multiplicant la columna de les freqüències relatives per ![]() . La suma de la columna és de
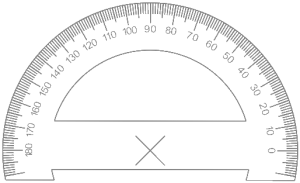
. La suma de la columna és de ![]() i té una utilitat exclusiva per a dibuixar el gràfic de sectors de forma manual amb el semicercle graduat o transportador d’angles, actualment qualsevol full de càlcul dibuixa el gràfic automàticament.
i té una utilitat exclusiva per a dibuixar el gràfic de sectors de forma manual amb el semicercle graduat o transportador d’angles, actualment qualsevol full de càlcul dibuixa el gràfic automàticament.
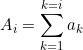 . La sisena columna conté els angles acumulats i el valor de cada fila es calcula sumant a cada angle els anteriors.
. La sisena columna conté els angles acumulats i el valor de cada fila es calcula sumant a cada angle els anteriors. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
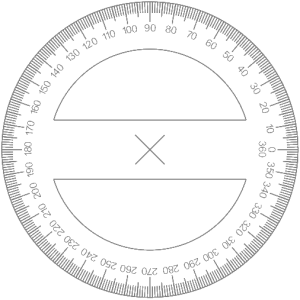
, ![]() . Aquesta columna és interessant per a dibuixar manualment el diagrama de sectors amb un cercle graduat o transportador complet d’angles.
. Aquesta columna és interessant per a dibuixar manualment el diagrama de sectors amb un cercle graduat o transportador complet d’angles.
El paràmetre estadístic
![]() . La moda és un valor de centralització estadístic i és el valor de la variable amb màxima freqüència,
. La moda és un valor de centralització estadístic i és el valor de la variable amb màxima freqüència, ![]() . Si existeix un empat de màximes freqüències parlareu d’estadístiques bimodals, trimodals…
. Si existeix un empat de màximes freqüències parlareu d’estadístiques bimodals, trimodals…
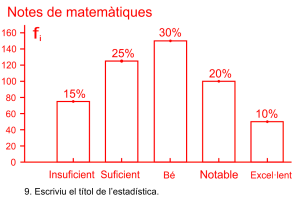
Representació del diagrama de barres
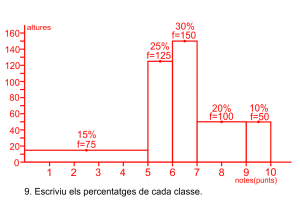
És un gràfic on les dades es representen amb rectangles separats i equidistants, del mateix ample i l’altura és proporcional a la freqüència. L’eix horitzontal té el nom dels valors de la variable estadística i l’eix vertical les freqüències. També podeu afegir en el centre de cada columna o en la part superior la freqüència relativa en percentatge.
Les notes de matemàtiques dels 500 alumnes de l’institut.
Fotograma anterior <clic en la part esquerra de la imatge>, fotograma posterior <clic en la part dreta de la imatge>
Per a comparar varies estadístiques es dibuixen en el mateix gràfic i totes les barres que representen la mateixa informació de cada estadística es dibuixen juntes, i cada estadística d’un color diferent.
Les marques de les freqüències poden fer-se amb el sistema ![]() és a dir, utilitzant els següents increments per a les ordenades:
és a dir, utilitzant els següents increments per a les ordenades: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , …
, …
La informació gràfica ha de ser molt visual i no es recomanen gràfics molt estrets o molt amples que impossibiliten una interpretació adequada de la informació.
Representació del diagrama de sectors
És un gràfic on les dades es representen amb sectors circulars seguint els següents procediments.
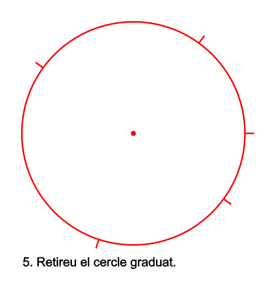
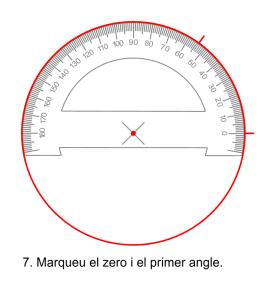
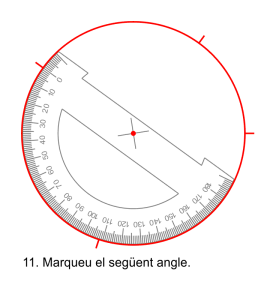
La forma més senzilla és amb un cercle graduat que permet dibuixar la circumferència i els angles acumulats sense moure el transportador. Aquest procediment no necessita moure l’aparell i per això és molt precís.
Les notes de matemàtiques dels 500 alumnes de l’institut.

Fotograma anterior <clic en la part esquerra de la imatge>, fotograma posterior <clic en la part dreta de la imatge>
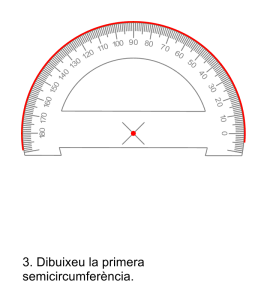
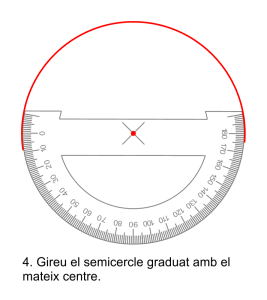
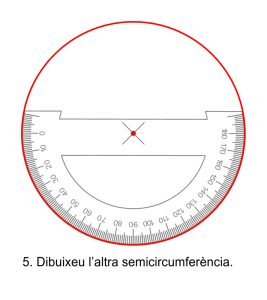
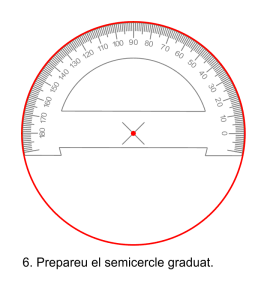
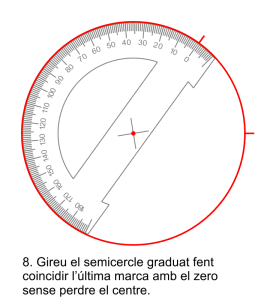
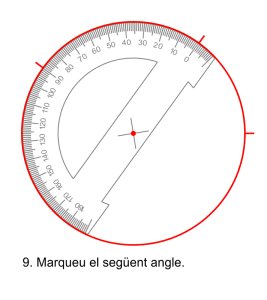
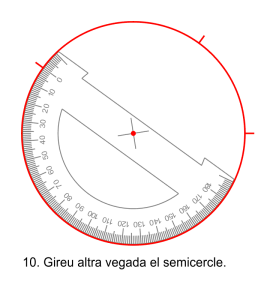
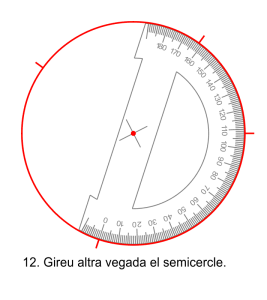
Amb el semicercle graduat el procediment és més llarg, requereix dibuixar dos semicircumferències, girar el transportador per a dibuixar cada angle i si els angle superen els ![]() necessitareu un altre gir per completar l’angle. Aquest procediment necessita girar moltes vegades l’aparell i per això és molt imprecís.
necessitareu un altre gir per completar l’angle. Aquest procediment necessita girar moltes vegades l’aparell i per això és molt imprecís.
Les notes de matemàtiques dels 500 alumnes de l’institut.

Fotograma anterior <clic en la part esquerra de la imatge>, fotograma posterior <clic en la part dreta de la imatge>
També podeu representar la informació en un semicercle, multiplicant les freqüències relatives per ![]() ,
, ![]() . Aquest gràfic és molt típic en la representació de les dades electorals municipals, autonòmiques i estatals.
. Aquest gràfic és molt típic en la representació de les dades electorals municipals, autonòmiques i estatals.
Programes informàtics
Hi ha infinitat d’aplicacions informàtiques que calculen i dibuixen estadístiques amb moltíssimes possibilitats de disseny, però he preferit utilitzar un programa que calcule solament les taules, les dades i els gràfics més bàsics. En el programa “Taules i gràfics estadístics“, creat amb GeoGebra, podeu introduir la informació, separant cada element amb comes de la forma següent.
1, Les notes de matemàtiques, Insuficient, 75, Suficient, 125, Bé, 150, Notable, 100, Excel·lent, 50
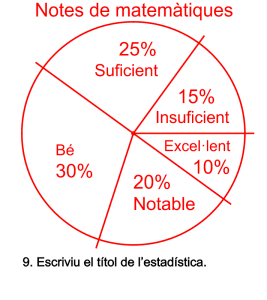
Primer escriviu el nombre 1 per informar al programa que es tracta d’una estadística qualitativa.
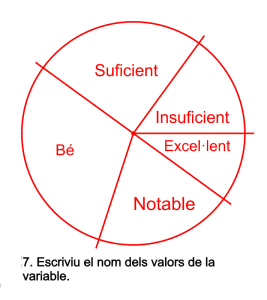
Després escriviu el títol de l’estadística.
I a continuació el nom de cada valor seguit de la seua freqüència.
Finalment pitgeu la tecla enter.
Ara disposareu de la taula, de les dades estadístiques, del gràfic de sectors amb dos controls per a modificar la grandària i el gràfic de barres amb tres control per a modificar l’altura i l’ample.

El model estadístic quantitatiu discret
Abans d’estudiar aquest model heu d’estudiar en profunditat el model qualitatiu.
La taula
Aquest model permet estudiar poblacions amb variables quantitatives discretes, variables que utilitzen els nombres naturals o enters. Per exemple, podeu estudiar la quantitat de germans, la quantitat de viatges realitzats.
Per analitzar la taula d’aquest model estadístic observareu l’exemple següent.
Les notes de matemàtiques dels 500 alumnes de l’institut.
| 1 | 5 | 0.01 | 1 | 1 | 3.6 | 3.6 | 5 | 123.008 |
| 2 | 10 | 0.02 | 2 | 3 | 7.2 | 10.8 | 20 | 156.816 |
| 3 | 20 | 0.04 | 4 | 7 | 14.4 | 25.5 | 60 | 175.232 |
| 4 | 40 | 0.08 | 8 | 15 | 28.8 | 54.0 | 160 | 153.664 |
| 5 | 125 | 0.25 | 25 | 40 | 90.0 | 144.0 | 625 | 115.200 |
| 6 | 150 | 0.30 | 30 | 70 | 108.0 | 252.0 | 900 | 0.240 |
| 7 | 60 | 0.12 | 12 | 82 | 43.2 | 295.2 | 420 | 64.896 |
| 8 | 40 | 0.08 | 8 | 90 | 28.8 | 324.0 | 320 | 166.464 |
| 9 | 30 | 0.06 | 6 | 96 | 21.6 | 345.6 | 270 | 277.248 |
| 10 | 20 | 0.04 | 4 | 100 | 14.4 | 360.0 | 200 | 326.432 |
| 500 | 1.00 | 100 | 360.0 | 2980 | 1559.200 |
![]() . La primera columna conté els valors que pot prendre la variable estadística. Els subíndex tenen el mateix significat que en el model qualitatiu, indicant a quina fila pertany la informació.
. La primera columna conté els valors que pot prendre la variable estadística. Els subíndex tenen el mateix significat que en el model qualitatiu, indicant a quina fila pertany la informació. ![]() .
.
![]() . La segona columna conté les freqüències absolutes, comptabilitza la quantitat d’individus que tenen la variable amb el mateix valor. També tenen subíndex,
. La segona columna conté les freqüències absolutes, comptabilitza la quantitat d’individus que tenen la variable amb el mateix valor. També tenen subíndex, ![]() . Aquesta columna i l’anterior representen el punt de partida del càlcul de la taula. Baix de la columna està la grandària de la mostra
. Aquesta columna i l’anterior representen el punt de partida del càlcul de la taula. Baix de la columna està la grandària de la mostra ![]() .
. ![]() .
.
![]() . La tercera columna conté les freqüències relatives, redueix tota l’estadística a la unitat, i és calcula dividint la freqüència absoluta entre la quantitat de mostra. Observeu que la suma de les freqüències relatives sempre és la unitat,
. La tercera columna conté les freqüències relatives, redueix tota l’estadística a la unitat, i és calcula dividint la freqüència absoluta entre la quantitat de mostra. Observeu que la suma de les freqüències relatives sempre és la unitat, ![]() .
.
![]() . La quarta columna conté les freqüències relatives en percentatge i es calcula multiplicant per
. La quarta columna conté les freqüències relatives en percentatge i es calcula multiplicant per ![]() les freqüències relatives. Observeu que la suma de les freqüències relatives en percentatge sempre és
les freqüències relatives. Observeu que la suma de les freqüències relatives en percentatge sempre és ![]() , i no oblideu que aquesta columna és la més utilitzada en els informes estadístics.
, i no oblideu que aquesta columna és la més utilitzada en els informes estadístics.
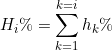 . La cinquena columna conté les freqüències relatives acumulades en percentatge i es calcula sumant a cada freqüència relativa en percentatge, totes les anteriors,
. La cinquena columna conté les freqüències relatives acumulades en percentatge i es calcula sumant a cada freqüència relativa en percentatge, totes les anteriors, ![]() ,
, ![]() ,
, ![]() … Aquesta columna és fonamental per a calcula la mediana, els quartils, i els percentils estadístics.
… Aquesta columna és fonamental per a calcula la mediana, els quartils, i els percentils estadístics.
![]() . La sisena columna conté els angles del gràfic de sectors. Es calcula multiplicant la columna de freqüències relatives per
. La sisena columna conté els angles del gràfic de sectors. Es calcula multiplicant la columna de freqüències relatives per ![]() . La suma de la columna és de
. La suma de la columna és de ![]() i té una utilitat exclusiva per a dibuixar manualment el gràfic de sectors amb el semicercle graduat o transportador d’angles.
i té una utilitat exclusiva per a dibuixar manualment el gràfic de sectors amb el semicercle graduat o transportador d’angles.
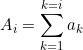 . La setena columna conté els angles acumulats i cada fila es calcula sumant-li els angles anteriors. Aquesta columna és interessant per a dibuixar manualment el diagrama de sectors amb un cercle graduat o transportador complet d’angles.
. La setena columna conté els angles acumulats i cada fila es calcula sumant-li els angles anteriors. Aquesta columna és interessant per a dibuixar manualment el diagrama de sectors amb un cercle graduat o transportador complet d’angles.
![]() . La huitena columna conté el producte de les dues primeres columnes, representa la quantitat de propietat que hi ha en una fila. La suma de la columna
. La huitena columna conté el producte de les dues primeres columnes, representa la quantitat de propietat que hi ha en una fila. La suma de la columna ![]() representa la quantitat total de propietat de l’estadística. Amb aquesta suma i la suma de freqüències podeu calcula la mitjana
representa la quantitat total de propietat de l’estadística. Amb aquesta suma i la suma de freqüències podeu calcula la mitjana ![]() , important per a calcular la columna següent.
, important per a calcular la columna següent.
![]() . La novena columna conté les desviacions elevades al quadrat dels valors, respecte de la mitjana. La suma de la columna
. La novena columna conté les desviacions elevades al quadrat dels valors, respecte de la mitjana. La suma de la columna ![]() representa el sumatori de totes les desviacions quadràtiques de les dades i permet calcular la desviació típica de l’estadística.
representa el sumatori de totes les desviacions quadràtiques de les dades i permet calcular la desviació típica de l’estadística.
Els paràmetres estadístics
![]() . La moda és un paràmetre de centralització i es calcula buscant el valor de la variable de màxima freqüència. Té les unitats de la variable,
. La moda és un paràmetre de centralització i es calcula buscant el valor de la variable de màxima freqüència. Té les unitats de la variable, ![]() .
.
![]() . La mitjana també és un paràmetre de centralització i es calcula dividint la quantitat de propietat entre la quantitat de mostra. La mitjana representa la quantitat de propietat que tindria un individu si poguéssiu repartir-la tota. També té les unitats de la variable,
. La mitjana també és un paràmetre de centralització i es calcula dividint la quantitat de propietat entre la quantitat de mostra. La mitjana representa la quantitat de propietat que tindria un individu si poguéssiu repartir-la tota. També té les unitats de la variable, ![]() .
.
![]() . La mediana és un paràmetre de centralització, és el valor que divideix la població en dos parts iguals. El primer
. La mediana és un paràmetre de centralització, és el valor que divideix la població en dos parts iguals. El primer ![]() de la població té una quantitat de propietat igual o inferior a la mediana i l’altre
de la població té una quantitat de propietat igual o inferior a la mediana i l’altre ![]() té una quantitat de propietat igual o superior a la mediana. Per a calcular la mediana heu de buscar el valor
té una quantitat de propietat igual o superior a la mediana. Per a calcular la mediana heu de buscar el valor ![]() en la columna de freqüències relatives acumulades en percentatge. Si existeix, calculeu la semisuma del valor de la variable d’aquesta línea i la següent,
en la columna de freqüències relatives acumulades en percentatge. Si existeix, calculeu la semisuma del valor de la variable d’aquesta línea i la següent, ![]() . Si no existeix, és el valor de la variable amb la freqüència acumulada en percentatge més petita superior a
. Si no existeix, és el valor de la variable amb la freqüència acumulada en percentatge més petita superior a ![]() ,
, ![]() . Evidentment té unitats,
. Evidentment té unitats, ![]() ,
, ![]() és el percentatge més petit superior a
és el percentatge més petit superior a ![]() i està en la sisena línea.
i està en la sisena línea.
![]() . El primer quartil és un paràmetre de posició, el valor que divideix la població en dos parts. El primer
. El primer quartil és un paràmetre de posició, el valor que divideix la població en dos parts. El primer ![]() de la població té una quantitat de propietat igual o inferior al primer quartil i l’altre
de la població té una quantitat de propietat igual o inferior al primer quartil i l’altre ![]() té una quantitat de propietat igual o superior al primer quartil. Per a calcular el primer quartil heu de buscar el valor
té una quantitat de propietat igual o superior al primer quartil. Per a calcular el primer quartil heu de buscar el valor ![]() en la columna de freqüències relatives acumulades en percentatge. Si existeix, calculeu la semisuma del valor de la variable d’aquesta línea i la següent,
en la columna de freqüències relatives acumulades en percentatge. Si existeix, calculeu la semisuma del valor de la variable d’aquesta línea i la següent, ![]() . Si no existeix, és el valor de la variable amb la freqüència acumulada en percentatge més petita superior a
. Si no existeix, és el valor de la variable amb la freqüència acumulada en percentatge més petita superior a ![]() ,
, ![]() . Evidentment té unitats,
. Evidentment té unitats, ![]() ,
, ![]() és el percentatge més petit superior a
és el percentatge més petit superior a ![]() i està en la cinquena línea.
i està en la cinquena línea.
![]() . El segon quartil és la mediana.
. El segon quartil és la mediana.
![]() . El tercer quartil és un paràmetre de posició, el valor que divideix la població en dos parts. El primer
. El tercer quartil és un paràmetre de posició, el valor que divideix la població en dos parts. El primer ![]() de la població té una quantitat de propietat igual o inferior al tercer quartil i l’altre
de la població té una quantitat de propietat igual o inferior al tercer quartil i l’altre ![]() té una quantitat de propietat igual o superior al tercer quartil. Per a calcula el tercer quartil heu de buscar el valor
té una quantitat de propietat igual o superior al tercer quartil. Per a calcula el tercer quartil heu de buscar el valor ![]() en la columna de freqüències relatives acumulades en percentatge. Si existeix, calculeu la semisuma del valor de la variable d’aquesta línea i la següent,
en la columna de freqüències relatives acumulades en percentatge. Si existeix, calculeu la semisuma del valor de la variable d’aquesta línea i la següent, ![]() . Si no existeix, és el valor de la variable amb la freqüència acumulada en percentatge més petita superior a
. Si no existeix, és el valor de la variable amb la freqüència acumulada en percentatge més petita superior a ![]() ,
, ![]() . Evidentment té unitats,
. Evidentment té unitats, ![]() ,
, ![]() és el percentatge més petit superior a
és el percentatge més petit superior a ![]() i està en la setena línea.
i està en la setena línea.
![]() . Els percentils són paràmetres de posició, el valor que divideix la població en dos parts. El primer
. Els percentils són paràmetres de posició, el valor que divideix la població en dos parts. El primer ![]() de la població té una quantitat de propietat igual o inferior a
de la població té una quantitat de propietat igual o inferior a ![]() i l’altre
i l’altre ![]() té una quantitat de propietat igual o superior a
té una quantitat de propietat igual o superior a ![]() . Per a calcular aquest valor heu de buscar el valor de
. Per a calcular aquest valor heu de buscar el valor de ![]() en la columna de freqüències relatives acumulades en percentatge. Si existeix, calculeu la semisuma del valor de la variable d’aquesta línea i la següent,
en la columna de freqüències relatives acumulades en percentatge. Si existeix, calculeu la semisuma del valor de la variable d’aquesta línea i la següent, ![]() . Si no existeix, és el valor de la variable amb la freqüència acumulada en percentatge més petita superior a
. Si no existeix, és el valor de la variable amb la freqüència acumulada en percentatge més petita superior a ![]() ,
, ![]() . Evidentment té unitats,
. Evidentment té unitats, ![]() , podeu observar el percentatge
, podeu observar el percentatge ![]() en la taula. No oblideu les igualtats:
en la taula. No oblideu les igualtats: ![]() ,
, ![]() , i
, i ![]() .
.
![]() . El rang és un paràmetre de dispersió, es calcula restant el valor màxim i el mínim de la variable. També té uniat
. El rang és un paràmetre de dispersió, es calcula restant el valor màxim i el mínim de la variable. També té uniat ![]() .
.
![]() . El rang interquartílic és interval que representa al
. El rang interquartílic és interval que representa al ![]() central de la mostra,
central de la mostra, ![]() .
.
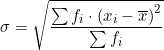 . La desviació típica representada per la lletra grega sigma minúscula
. La desviació típica representada per la lletra grega sigma minúscula ![]() , és un paràmetre de dispersió que mesura la mitjana de les desviacions quadràtiques, es calcula amb l’arrel de la divisió de l’última columna entre la suma de les freqüències. També té unitats,
, és un paràmetre de dispersió que mesura la mitjana de les desviacions quadràtiques, es calcula amb l’arrel de la divisió de l’última columna entre la suma de les freqüències. També té unitats, ![]() . Permet determinar la homogeneïtat d’una estadística, si el valor és nul l’estadística és totalment homogènia i conforme creix és menys homogènia o més heterogènia. També permet comparar estadístiques amb les mateixes unitats.
. Permet determinar la homogeneïtat d’una estadística, si el valor és nul l’estadística és totalment homogènia i conforme creix és menys homogènia o més heterogènia. També permet comparar estadístiques amb les mateixes unitats.
![]() . El rang mitjà és l’interval centrat en la mitjana que inclou aproximadament el
. El rang mitjà és l’interval centrat en la mitjana que inclou aproximadament el ![]() de les dades,
de les dades, ![]() .
.
![]() . L’entorn mitjà, és una altra forma d’expressar el rang mitjà.
. L’entorn mitjà, és una altra forma d’expressar el rang mitjà. ![]() .
.
![]() . El coeficient de variació és un paràmetre de dispersió, es calcula amb el quocient de la desviació típica entre la mitjana. Les característiques són similars a la desviació típica, però amb un avantatge important, no té unitats i per això, permet comparar la homogeneïtat o heterogeneïtat de qualsevol estadística,
. El coeficient de variació és un paràmetre de dispersió, es calcula amb el quocient de la desviació típica entre la mitjana. Les característiques són similars a la desviació típica, però amb un avantatge important, no té unitats i per això, permet comparar la homogeneïtat o heterogeneïtat de qualsevol estadística, ![]() .
.
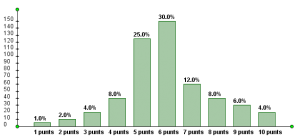
Representació del diagrama de barres
És un gràfic amb les mateixes característiques del model qualitatiu.
Les notes de matemàtiques dels 500 alumnes de l’institut.
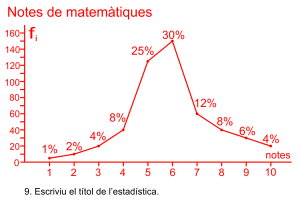
Representació del polígon de freqüències
És un gràfic amb les mateixes característiques que el de barres, però substituint els rectangles per una línea trencada que uneix els centres dels costats superiors dels rectangles. Aquest tipus de gràfics s’utilitzen molt per a models amb variables temporals.
Les notes de matemàtiques dels 500 alumnes de l’institut.

Fotograma anterior <clic en la part esquerra de la imatge>, fotograma posterior <clic en la part dreta de la imatge>
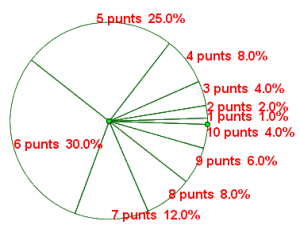
Representació del diagrama de sectors
És un gràfic amb les mateixes característiques del model qualitatiu.
Les notes de matemàtiques dels 500 alumnes de l’institut.
Programes informàtics
També podeu utilitzar el programa d’estadística “Taules i gràfics estadístics“, creat amb GeoGebra, podeu introduir la informació, separant cada element amb comes de la forma següent.
2, Les notes de matemàtiques, punts, 1, 5, 2, 10, 3, 20, 4, 40, 5, 125, 6, 150, 7, 60, 8, 40, 9, 30, 10, 20
Primer, escriviu el nombre 2 per informar que es tracta d’una estadística quantitativa discreta.
Després escriviu el títol de l’estadística.
A continuació la unitat.
Finalment els valors seguits de la seua freqüència.
Una vegada cliqueu enter, disposareu de la taula, les dades estadístiques, el gràfic de sectors amb dos punts de controls per a modificar la grandària, el gràfic de barres i el poligonal amb tres punts de control per a modificar l’altura i l’ample.
Les notes de matemàtiques dels 500 alumnes de l’institut.

La calculadora científica
Totes les calculadores científiques tenen un mòdul estadístic adaptat als models estadístics quantitatius discrets. En aquesta explicació s’utilitzen les calculadores CASIO fx 570 SP X i CASIO fx 991 SP X.
Activeu la columna de freqüències: ![]()
![]()

![]()

![]()
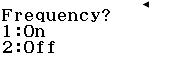
![]()
Entreu al mòdul estadístic (entrareu directament en l’editor estadístic): ![]()

![]()
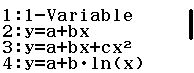
![]()
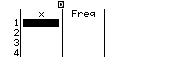
Escriviu les dades en les columnes de valors i de freqüències, després de cada nombre cliqueu el botó ![]() i desplaceu-vos amb les tecles de desplaçament.
i desplaceu-vos amb les tecles de desplaçament. 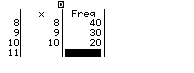
Sortiu de l’editor estadístic sense sortir del mòdul estadístic per a fer càlculs: ![]()

Podeu tornat a entrar en l’editor estadístic per a modificar les dades en qualsevol moment: ![]()

![]()
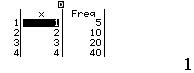
Podeu observar els paràmetres estadístics: ![]()

![]()
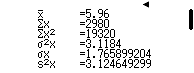
![]()
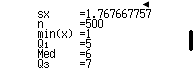
![]()
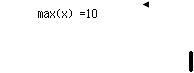
Podeu calcular el rang: ![]()

![]()
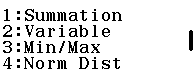
![]()
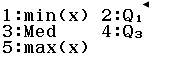
![]()
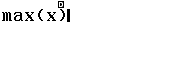
![]()
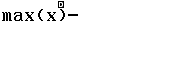
![]()

![]()
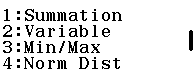
![]()
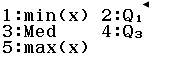
![]()
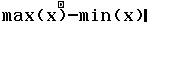
![]()
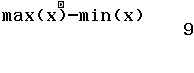
Podeu calcular el coeficient de variació: ![]()

![]()
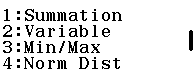
![]()

![]()

![]()

![]()

![]()
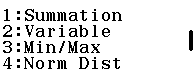
![]()

![]()

![]()
Podeu sortir del mòdul estadístic entrant en altre mòdul (s’esborraran les dades estadístiques): ![]()
![]() .
.
El model estadístic quantitatiu continu
Abans d’estudiar aquest model heu d’estudiar en profunditat el model quantitatiu discret.
La taula
Aquest model permet estudiar poblacions amb variables quantitatives contínues, variables que utilitzen els nombres racionals o reals. Per exemple, podeu estudiar els ingressos econòmics de les persones, les altures de les persones, les temperatures de les poblacions.
En aquestes estadístiques la varietat de valors és extraordinària, si cada valor s’escriu en una línea, necessitaríeu taules molt llargues. Per a simplificar els càlculs, s’agrupen les dades en intervals. Els intervals han de ser incompatibles, es a dir, no han de tenir elements comuns, i la unió de tots els intervals ha de representar a tota l’estadística. Cada valor solament pot ser d’una única classe estadística. Si un interval finalitza obert, el següent ha de començar tancat i viceversa. La selecció dels intervals afecta als resultats estadístics.
Hi ha un parell de fòrmules per determinar una recomanació de la quantitat d’intervals i l’amplitud, però s’ha de considerar simplement una recomanació i utilitzar aquets valors de forma prudent.
![]() indica la quantitat d’intervals.
indica la quantitat d’intervals.
![]() indica l’ample dels intervals.
indica l’ample dels intervals.
En el nostre exemple ![]() i
i ![]() que podriem aproximar a 20 intervals de 0,5 punts d’ample, però en aquest cas els intervals queden establerts per la tradició normativa del sistema educatiu.
que podriem aproximar a 20 intervals de 0,5 punts d’ample, però en aquest cas els intervals queden establerts per la tradició normativa del sistema educatiu.
Per analitzar la taula d’aquest model estadístic observareu l’exemple següent. Ara les notes de l’alumnat tenen decimals i aquestes s’agrupen en intervals, per exemple ![]() ,
, ![]()
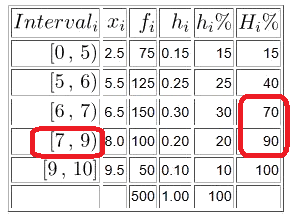
Les notes de matemàtiques dels 500 alumnes de l’institut.
| 2.5 | 75 | 0.15 | 15 | 15 | 15 | 54 | 54 | 187.5 | 1054.6875 | |
| 5.5 | 125 | 0.25 | 25 | 40 | 125 | 90 | 144 | 687.5 | 70.3125 | |
| 6.5 | 150 | 0.30 | 30 | 70 | 150 | 108 | 252 | 975.0 | 9.3750 | |
| 8.0 | 100 | 0.20 | 20 | 90 | 50 | 72 | 324 | 800.0 | 306.2500 | |
| 9.5 | 50 | 0.10 | 10 | 100 | 50 | 36 | 360 | 475.0 | 528.1250 | |
| 500 | 1.00 | 100 | 360 | 3125.0 | 1968.7500 |
![]() . La primera columna conté totes les classes en forma d’intervals
. La primera columna conté totes les classes en forma d’intervals ![]() . El primer nombre és l’extrem inferior i el segon l’extrem superior. L’extrem superior d’una classe ha de coincidir amb l’extrem inferior de la següent, un extrem ha de ser obert i l’altre tancat.
. El primer nombre és l’extrem inferior i el segon l’extrem superior. L’extrem superior d’una classe ha de coincidir amb l’extrem inferior de la següent, un extrem ha de ser obert i l’altre tancat.
![]() . La segona columna conté les marques de classe i es calcula amb la semisuma dels extrems de l’interval. Per exemple
. La segona columna conté les marques de classe i es calcula amb la semisuma dels extrems de l’interval. Per exemple ![]() . Aquesta columna és la utilitzada per a introduir la informació en les calculadores.
. Aquesta columna és la utilitzada per a introduir la informació en les calculadores.
![]() . La tercera columna conté la freqüència absoluta de cada classe, i la suma és la quantitat de mostra,
. La tercera columna conté la freqüència absoluta de cada classe, i la suma és la quantitat de mostra, ![]() .
.
![]() . La quarta columna conté les freqüències relatives.
. La quarta columna conté les freqüències relatives.
![]() . La cinquena columna conté les freqüències relatives en percentatge.
. La cinquena columna conté les freqüències relatives en percentatge.
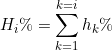 . La sisena columna conté les freqüències relatives acumulades en percentatge.
. La sisena columna conté les freqüències relatives acumulades en percentatge.
![]() . La setena columna conté l’altura dels rectangles en l’histograma. L’histograma és un gràfic amb rectangles de base variable i l’àrea proporcional a la freqüència. Com l’àrea d’un rectangle és base per altura,
. La setena columna conté l’altura dels rectangles en l’histograma. L’histograma és un gràfic amb rectangles de base variable i l’àrea proporcional a la freqüència. Com l’àrea d’un rectangle és base per altura, ![]() , podeu aïllar l’altura,
, podeu aïllar l’altura, ![]() . L’àrea és la freqüència i la base l’ample de la classe.
. L’àrea és la freqüència i la base l’ample de la classe.
![]() . La huitena columna conté els angles dels sectors.
. La huitena columna conté els angles dels sectors.
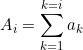 . La novena columna conté els angles acumulats.
. La novena columna conté els angles acumulats.
![]() . La desena columna conté la quantitat de propietat de cada classe. Amb la mitjana
. La desena columna conté la quantitat de propietat de cada classe. Amb la mitjana ![]() podeu calcular la columna següent.
podeu calcular la columna següent.
![]() . La onzena columna conté la desviació quadràtica de la classe.
. La onzena columna conté la desviació quadràtica de la classe.
Els paràmetres estadístics
![]() . La moda es calcula buscant el valor de la variable de màxima freqüència, podeu expressar aquest valor en forma d’interval (interval modal)
. La moda es calcula buscant el valor de la variable de màxima freqüència, podeu expressar aquest valor en forma d’interval (interval modal) ![]() , o amb la marca de classe,
, o amb la marca de classe, ![]()
![]() . La mitjana,
. La mitjana, ![]() . L’interval mitjà és el que inclou la mitjana,
. L’interval mitjà és el que inclou la mitjana, ![]()
![]() . El rang, es calcula restant el extrem superior de l’última classe i l’extrem inferior de la primera classe.
. El rang, es calcula restant el extrem superior de l’última classe i l’extrem inferior de la primera classe. ![]() .
.
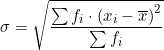 . La desviació típica,
. La desviació típica, ![]() .
.
![]() . El rang mitjà,
. El rang mitjà, ![]() .
.
![]() . L’entorn mitjà, és altra forma d’expressar el rang mitjà,
. L’entorn mitjà, és altra forma d’expressar el rang mitjà, ![]() .
.
![]() . El coeficient de variació,
. El coeficient de variació, ![]() .
.
La mediana o percentil 50 ![]() , el primer quartil o percentil 25
, el primer quartil o percentil 25 ![]() , el tercer quartil o percentil 75
, el tercer quartil o percentil 75 ![]() i la resta de percentils es calculen per interpolació lineal del polígon de freqüències relatives en percentatge, que voreu després d’estudiar el gràfic.
i la resta de percentils es calculen per interpolació lineal del polígon de freqüències relatives en percentatge, que voreu després d’estudiar el gràfic.
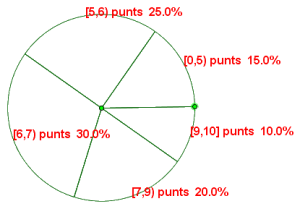
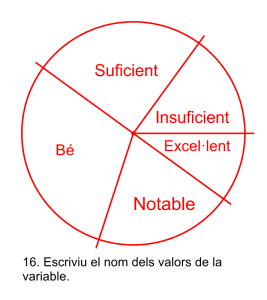
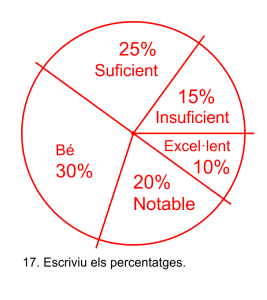
Representació del diagrama de sectors
És un gràfic amb les mateixes característiques del model qualitatiu i del model quantitatiu discret.
Les notes de matemàtiques dels 500 alumnes de l’institut.
Representació de l’histograma
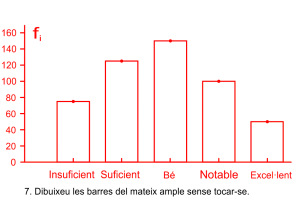
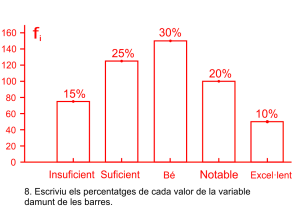
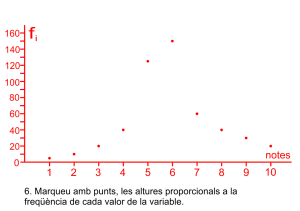
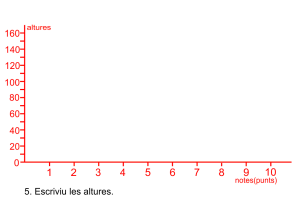
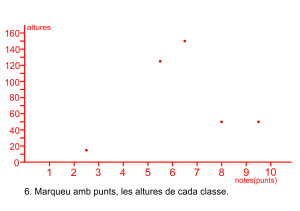
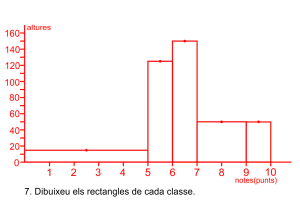
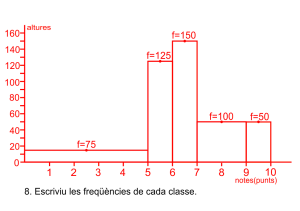
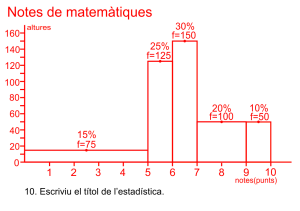
Prepareu l’eix abscisses amb una partició que represente tots els intervals, de forma proporcional a la seua grandària de forma contínua, prepareu l’eix d’ordenades amb intervals fins l’altura màxima. Dibuixeu els rectangles i escriviu en la part superior de cada classe la freqüència absoluta i la relativa en percentatge.
Les notes de matemàtiques dels 500 alumnes de l’institut.

Fotograma anterior <clic en la part esquerra de la imatge>, fotograma posterior <clic en la part dreta de la imatge>
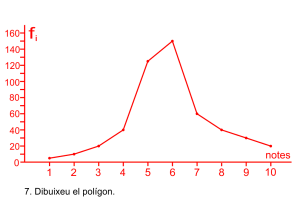
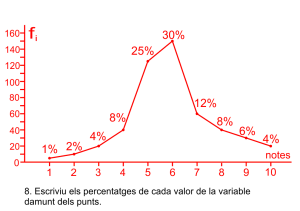
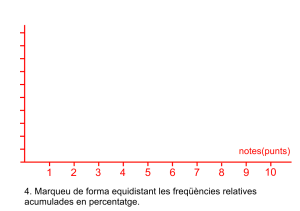
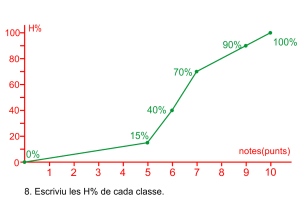
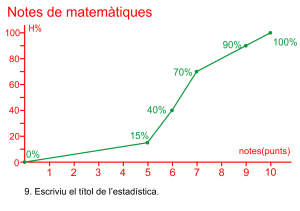
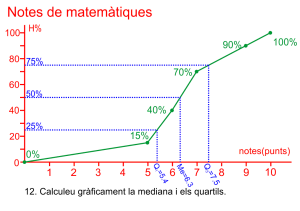
Representació del polígon de freqüències relatives acumulades en percentatge
Prepareu l’eix abscisses amb una partició que represente tots els intervals, de forma proporcional a la seua grandària de forma contínua, prepareu l’eix d’ordenades amb intervals des del zero fins al 100.
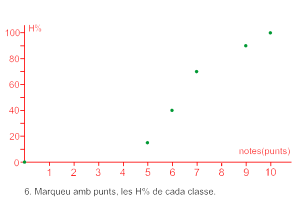
Marqueu el primer punt ![]() , en el primer extrem inferior i altura zero.
, en el primer extrem inferior i altura zero.
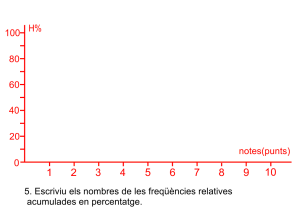
Marqueu la resta de punts amb els valors de la columna de freqüències relatives acumulades en percentatge. ![]() .
.
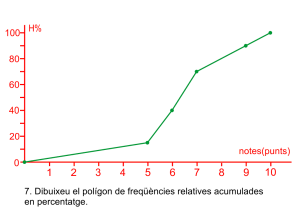
Uniu en una línea poligonal els punts. Evidentment el gràfic comença en una altura zero i finalitza en una altura 100.
Les notes de matemàtiques dels 500 alumnes de l’institut.

Fotograma anterior <clic en la part esquerra de la imatge>, fotograma posterior <clic en la part dreta de la imatge>
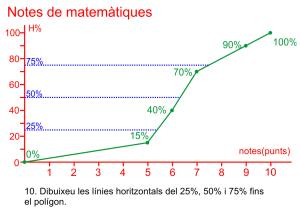
Càlcul de percentils
![]() . El percentil zero és l’extrem inferior de la primera classe.
. El percentil zero és l’extrem inferior de la primera classe.
![]() . El percentil cent és l’extrem superior de l’última classe.
. El percentil cent és l’extrem superior de l’última classe.
![]() . Si el percentatge apareix en la columna de freqüències relatives acumulades en percentatge, el percentil és l’extrem superior de l’interval.
. Si el percentatge apareix en la columna de freqüències relatives acumulades en percentatge, el percentil és l’extrem superior de l’interval.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
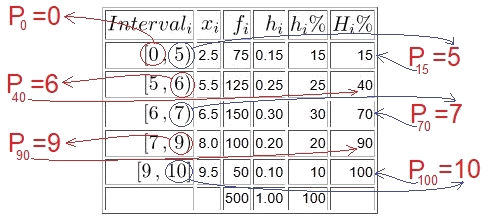
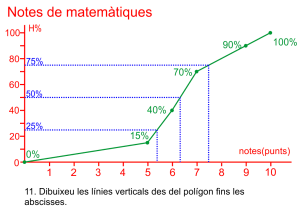
Per a la resta de percentils heu d’interpolar en el segment on estiga el percentatge més petit que supere al buscat ![]() .
.
![]() si el percentatge està en la primera classe.
si el percentatge està en la primera classe.
![]()
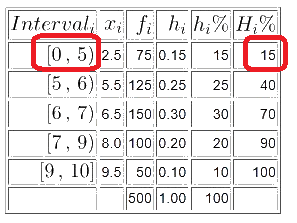
Resulta molt difícil recordar aquesta fórmula, però sencill recordar l’expressió contínua d’una recta ![]() .
.
Aquest interval té dos punts coneguts el ![]() i
i ![]()
Substituint en l’equació de la recta ![]() . Ara podeu calcular les notes substituint percentatges o calcular percentatges substituin notes.
. Ara podeu calcular les notes substituint percentatges o calcular percentatges substituin notes.
![]() si el percentatge està en altra classe.
si el percentatge està en altra classe.
![]()
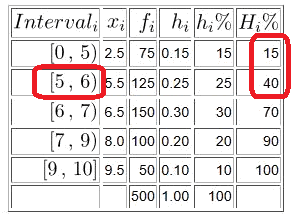
Aquest interval té dos punts coneguts el ![]() i
i ![]()
Substituint en l’equació de la recta ![]() . Ara podeu calcular les notes substituint percentatges o calcular percentatges substituin notes.
. Ara podeu calcular les notes substituint percentatges o calcular percentatges substituin notes.
En el cas particular del primer quartil ![]()
![]()
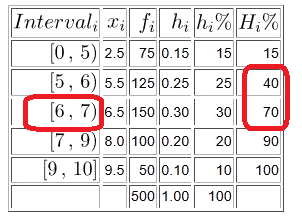
Aquest interval té dos punts coneguts el ![]() i
i ![]()
Substituint en l’equació de la recta ![]() . Ara podeu calcular les notes substituint percentatges o calcular percentatges substituin notes.
. Ara podeu calcular les notes substituint percentatges o calcular percentatges substituin notes.
En el cas particular de la mediana ![]() .
.
![]()
Aquest interval té dos punts coneguts el ![]() i
i ![]()
Substituint en l’equació de la recta ![]() . Ara podeu calcular les notes substituint percentatges o calcular percentatges substituin notes.
. Ara podeu calcular les notes substituint percentatges o calcular percentatges substituin notes.
En el cas particular del tercer quartil ![]() .
.
![]() . El rang interquartílic,
. El rang interquartílic, ![]() .
.
Programes informàtics
En aquest cas, també podeu utilitzar el programa d’estadística “Taules i gràfics estadístics“, creat amb GeoGebra, la informació la separareu amb comes de la forma següent.
3, Les notes de matemàtiques, punts, [0,5), 75, [5,6), 125, [6,7), 150, [7,9), 100, [9,10], 50
Primer, escriviu el nombre 3 per informar que es tracta d’una estadística quantitativa contínua.
Després escriviu el títol de l’estadística.
A continuació la unitat.
Finalment els intervals seguits de la seua freqüència. Cada interval comença on finalitza l’anterior.
Una vegada cliqueu enter, disposareu de la taula, les dades estadístiques, el gràfic de sectors amb dos punts de control per a modificar la grandària, l’histograma i el polígon de freqüències amb tres punts de control per a modificar l’altura i l’ample. Sobre la línea poligonal apareix un punt lliscant que permet calcular percentils.
Les notes de matemàtiques dels 500 alumnes de l’institut.

La calculadora científica
Avis important!
Les calculadores científiques bàsiques no tenen un mòdul estadístic adaptat al model estadístic quantitatiu continu, per tant el seu ús queda restringit al càlcul de la mitjana i la desviació típica. No oblideu d’introduir en la columna de les dades, les marques de classe.
El primer quartil, la mediana i el tercer quartil no estan calculats amb les interpolacions del gràfic de freqüències relatives acumulades en percentatge.










Deixa un comentari