Matemàtiques 0.1 fins l'infinit

És un mecanisme de la càmera situat entre les lents, que determina la quantitat de llum que entra en la càmera, controlat amb un sistema de làmines. Afecta especialment a la profunditat de camp de la fotografia, tancant el diafragma la profunditat de camp augmenta.

Modelització d’un diafragma fotogràfic

Es tracta de construir un diafragma fotogràfic dins d’una circumferència de radi equivalent al d’un sensor fotogràfic “full frame”, equivalent als negatius de 24mm per 36mm, que representa la part interna d’un objectiu fotogràfic.

El triangle curvilini i l’estrella curvilínia

Obriu una sessió de GeoGebra i anomeneu “DiafragmaFotogràfic1.ggb” al document.

Representeu l’origen O = (0, 0), el punt A = (sqrt(24² + 36²) / 2, 0) per on passa la circumferència, la semirecta de referència s1: Semirecta(O, A) i la circumferència c1: Circumferència(O, A) que representa la part interna de l’objectiu fotogràfic.

Prepareu el punt lliscant n:PuntLliscant(3,16,1,1,200,false,true,false,false) que representa la quantitat de làmines que formen el diafragma. Els valors representen el mínim, el màxim, l’increment, la velocitat, l’amplada, si és un angle, si és horitzontal, si l’animació esta activada i si es tracta d’un punt lliscant de valors aleatoris.

El diafragma està format per n làmines que tenen la forma de triangle curvilini, els tres costats amb el mateix radi unitat de l’objectiu, dos arcs de 60º i el tercer de 360º/n.

Dibuixeu els punts següents: N = Rotació(A, -60°, O) és el centre de l’arc inferior, M = Rotació(A, 360° / n, O) és l’extrem de l’arc de la dreta i N’ = Rotació(N, 360° / n, O) és el centre de l’arc superior.

Dibuixeu els tres arcs: el de la dreta a1: ArcDeCircumferència(O, A, M), el de l’esquerre a2: ArcDeCircumferència(N’, M, O) i el de baix a3: ArcDeCircumferència(N, A, O).

 

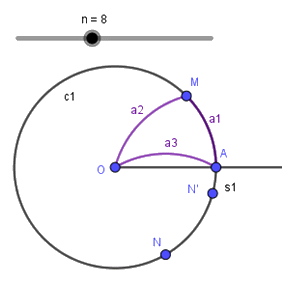
Quan la làmina està totalment oberta, el punt M és el més exterior, per tant el segment NM representa el radi de la circumferència exterior de l’objectiu c2:Circumferència(O, Distància(N, M)), creant una corona circular que inclourà el mecanisme de rotació i les làmines quan el diafragma està totalment obert.

Prepareu el mecanisme de rotació simulat amb una circumferència tangent a la corona i a la prolongació del tercer arc. Dibuixeu tres circumferències auxiliars per a determinar el centre de gir de la làmina i els punts de tangència: B = Intersecció(c2, s1) , C = PuntMitjà(A, B) , c3: Circumferència(O, C) , c4: Circumferència(N, Distància(O, C)) , D = Intersecció(c3, c4, 1) , c6: Circumferència(D, Distància(A, C)) i els dos punts de tangència E = Intersecció(c6, c1) i F = Intersecció(c6, c5) .

Ara dibuixeu l’arc que representa el mecanisme de gir a4: ArcDeCircumferència(D, F, E). Actualitzeu el primer arc des de la seua finestra de propietats, canviant el punt A pel punt E, ArcDeCircumferència(O, E, M), i des de la finestra de propietats del tercer arc l’allargueu-lo canviant el punt A pel punt F, ArcDeCircumferència(N, F, O).

Ara representeu l’angle màxim que pot girar el mecanisme que és inferior a 60º degut a que no gira respecte del punt A, β = Angle(E, D, F). I un punt lliscant per a seleccionar l’angle de gir desitjat, α: PuntLliscant(0º, β, 0.01º, 1, 200, true, true, false, false).

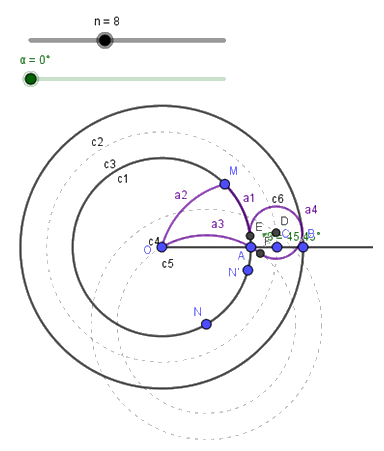
Activeu en la segona finestra gràfica les circumferències c1 i c2, dibuixeu també en la segona finestra gràfica tots els punts de gir de les làmines, pg = Seqüència(Rotació(D, k 360° / n, O), k, 0, n – 1).

També representeu tots els arcs en la segona finestra gràfica:
La1 = Seqüència(Rotació(Rotació(a1, k 360° / n, O), α, Element(pg, k + 1)), k, 0, n – 1)
La2 = Seqüència(Rotació(Rotació(a2, k 360° / n, O), α, Element(pg, k + 1)), k, 0, n – 1)
La3 = Seqüència(Rotació(Rotació(a3, k 360° / n, O), α, Element(pg, k + 1)), k, 0, n – 1)
La4 = Seqüència(Rotació(Rotació(a4, k 360° / n, O), α, Element(pg, k + 1)), k, 0, n – 1)

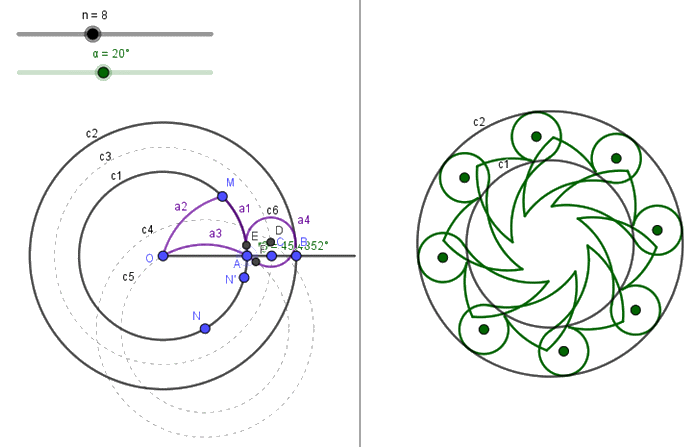
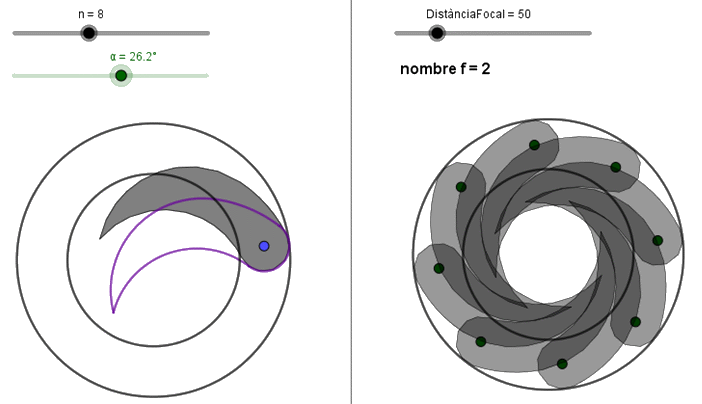
Podeu observar que n làmines tanquen perfectament l’objectiu, però formen entre totes una pupil·la en forma d’estrella curvilínia durant l’apertura i tancament del diafragma, i en els objectius fotogràfics normalment formen un polígon curvilini de n costats.

 

Urpes i el polígon curvilini

Guardeu el document “DiafragmaFotogràfic1.ggb” i torneu-lo a guardar amb el nom “DiafragmaFotogràfic2.ggb”.

Amplieu la làmina per a tapar les puntes curvilínies de la pupil·la del diafragma.

Per emular la làmina començareu per allargar el tercer arc amb el punt O’ = Rotació(O, 360° / n, N)  modificant en la finestra de propietats el límit del tercer arc, canviant el punt O pel punt O’, ArcDeCircumferència(N, F, O’).

Per a desplaçar el segon arc prepareu el punt G = Intersecció(Mediatriu(M, O’), Recta(M, N)) i en la finestra de propietats modifiqueu el segon arc canviant el punt N’ pel punt G i el punt O pel punt O’, ArcDeCircumferència(G, M, O’).

Reduïu el quart arc a una semicircumferència, F’ = Simetria(F, D) i en la finestra de propietats modifiqueu el punt E del quart arc pel punt F’, ArcDeCircumferència(D, F, F’).

Solament queda modificar en la finestra de propietats del primer arc el punt O pel punt N i el punt E pel punt F’, ArcDeCircumferència(N, F’, M).

 

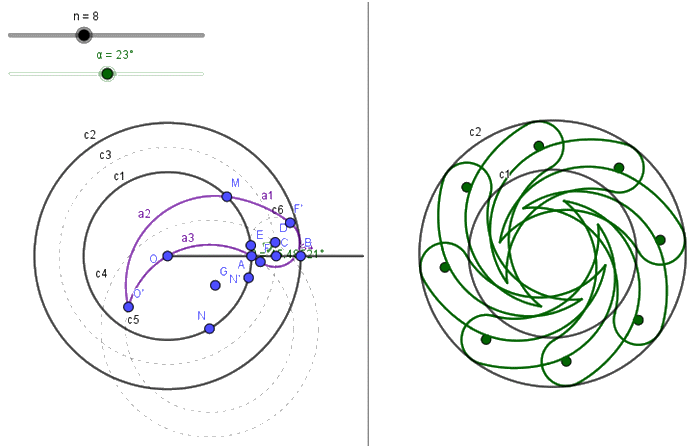
Polígons

Guardeu el document “DiafragmaFotogràfic2.ggb” i torneu-lo a guardar amb el nom “DiafragmaFotogràfic3.ggb”.

Ara utilitzeu els arcs per a crear un polígon i poder donar color a les làmines del diafragma. La creació de punts en els arcs presenta el problema de clicar interseccions i que el punt estiga associat a més d’un objecte, una estratègia consisteix en ampliar el dibuix amb el “zoom”, ocultar els elements que molesten, clicar els arcs en zones sense interseccions i a continuació arrossegar els punts en posicions adequadament distribuïdes, sense oblidar d’anomenar-los adequadament. El punt O no pot formar part del polígon degut a que el seu moviment respecte de l’arc és diferent a la resta de punts.

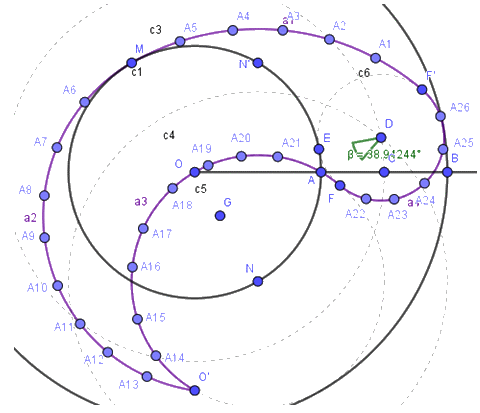
Per a generar el polígon sense acumular una quantitat impressionat d’objectes l’heu de definir-lo dins d’una llista, P = {Polígon(A1, A2, A3, A4, A5, M, A6, A7, A8, A9, A10, A11, A12, A13, O’, A14, A15, A16, A17, A18, A19, A20, A21, A, F, A22, A23, A24, A25, A26, F’)}.

Ara simplement queda transformar el polígon en una llista de polígons situats en la segona finestra gràfica per a simular el diafragma. LP = Seqüència(Rotació(Rotació(P, k 360° / n, O), -α, Element(pg, k + 1)), k, 0, n – 1) i esborrar les llistes La1, La2, La3 i La4.

Podeu donar moviment a la làmina de la part esquerra, LP2 = Rotació(P, -α, D), i ocultar els punts exceptuant el punt D, les circumferències exceptuant c1 i c2, l’angle β i la semirecta s1.

 

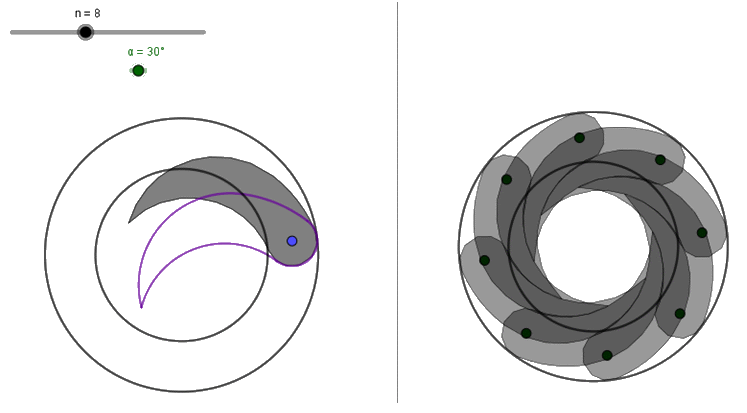
El nombre f

Guardeu el document “DiafragmaFotogràfic3.ggb” i torneu-lo a guardar amb el nom “DiafragmaFotogràfic4.ggb”.

El nombre_f és la mesura de l’obertura del diafragma. Els valors típics que observareu en un objectiu són una part de las llista {1, 1.4, 2, 2.8, 4, 5.6, 8, 11, 16, 22, 32…} i cada nombre_f representa una obertura del diafragma que permet la entrada de la meitat de llum que el nombre anterior. Per tant, quan més gran és el nombre_f més tancat està el diafragma i menys llum entra a la càmera.

El nombre_f és la raó entre la distància focal de l’objectiu, donat en mil·límetres i el diàmetre d’obertura del diafragma, també en mil·límetres, resultant un valor sense unitats, nombre_f=distància_focal/diàmetre_diafragma.

Per a representar la distància focal de l’objectiu utilitzareu un punt lliscant, DistànciaFocal:PuntLliscant(10, 200, 5, 1, 200, false, true, false, false), situat en la segona finestra gràfica.

El diàmetre d’obertura del diafragma no és constant per tractar-se d’un polígon curvilini, però podeu calcular el diàmetre d’una circumferència que tinga la mateixa àrea.

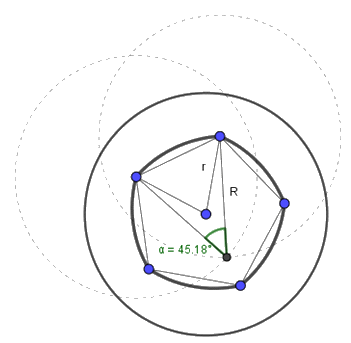
El polígon curvilini està format per un polígon regular de radi r i n segments circulars del mateix radi que l’objectiu. Necessiteu dibuixar tres circumferències dinàmiques: d1: Rotació(c5, -α, D), d2: Rotació(d1, 365° / n, O) i d3: Rotació(d2, 365° / n, O).

A continuació les primeres interseccions de les circumferències i el centre de la segona: H1 = Intersecció(d1, d2, 1), H2 = Intersecció(d2, d3, 1) i H3 = Centre(d2).

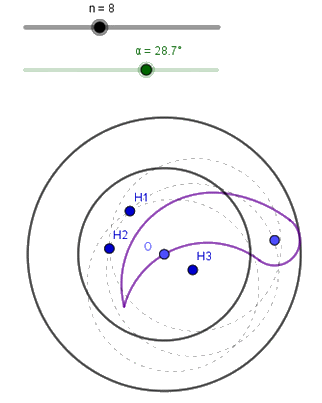
L’àrea del polígon curvilini serà n vegades el la del triangle (H1,H2,O) més n vegades la del segment circular (H1,H2,H3), ÀreaDiafragma = n Àrea(Polígon(H1, H2, O)) + n Àrea(ArcDeCircumferència(H3, H1, H2)).

El diàmetre d’una circumferència de la mateixa àrea el podeu calcular amb la fórmula DiàmetreDiafragma = sqrt(4 ÀreaDiafragma / π), l’obertura del diafragma amb l’expressió nombre_f = DistànciaFocal / DiàmetreDiafragma, i finalment heu d’escriure el valor en la segona finestra gràfica, t1 = “nombre f = ” + nombre_f.

Quan el diafragma està totalment obert les circumferències són coincidents i no és possible calcular els punts d’intersecció, també en la realitat les làmines no poden tancar totalment, per estar solapades cada una damunt de la següent. Per a resoldre aquests problemes modificareu en la finestra de propietats del punt lliscant α el valor inicial a 2° i el valor final a β – 0.001°.

Guardeu el document “DiafragmaFotogràfic4.ggb”.