Curs d’iniciació de GeoGebra per l’alumnat de matemàtiques d’ESO
Tipus: taller per a la IV Jornada de GeoGebra de la Comunitat Valenciana, “GeoGebra, instrument per a la didàctica de la matemàtica, Gandia 23-9-2017”.
Títol de la ponència: Curs d’iniciació de GeoGebra per l’alumnat de 6è de primària i 1r d’ESO.
Nivell educatiu: primària i secundària.
Idioma de la ponència: valencià.
Paraules clau: geometria dinàmica, GeoGebra, curs d’iniciació, autoavaluació, moodle.
Autor: Couchoud Pérez, Juan Manuel.
Correu electrònic: juan.manuel.couchoud@gmail.com
Currículum i institució: Professor de matemàtiques de l’IES Vall de la Safor, membre de la Societat d’Educació Matemàtica de la Comunitat Valenciana Al-Khwārizmī i vocal de l´Institut GeoGebra Valencià. Dedicat a la formació del professorat en Moodle, Màxima i actualment en GeoGebra.
Objectiu general del treball: El curs de GeoGebra pretén iniciar a l’alumnat en la utilització de les ferramentes i comandaments del programari GeoGebra i facilitar d’aquesta manera l’estudi, la investigació i la resolució de problemes geomètrics.
Material: còpies de seguretat del curs-moodle (data d’actualizació 31/8/2019). No oblideu descomprimir els documents abans d’utilitzar-los. La versió en català és backup-moodle2-course-2-gg00ca-20190831-1855-nu.zip, la versió en castellà és backup-moodle2-course-3-gg00es-20190903-1553-nu.zip i la versió en anglés és backup-moodle2-course-5-gg00en-20190831-1856-nu.zip.
El material també està disponible en la pàgina web de GeoGebra. La versió en català en https://www.geogebra.org/m/rpN4xDde, la versió en castellà https://www.geogebra.org/m/jCWGdJCQ en i la versió en anglés en https://www.geogebra.org/m/tYSyz3N8.
Presentació: Curs de GeoGebra per l’alumnat.ppsx , Curs de GeoGebra per l’alumnat.pdf .
Resum: La geometria de primària i secundària està molt centrada en la identificació i relacions de figures geomètriques, en els càlculs aritmètics, per a resoldre triangles i calcular perímetres, àrees i volums. És una geometria estàtica, sense moviment. GeoGebra ens porta a un canvi en la forma de treballar amb la geometria, ens dóna moviment, ens permet experimentar múltiples possibilitats, permet que la geometria dinàmica entre en les aules.
La introducció d’un nou recurs didàctic en la resolució de problemes implica que l’alumnat ha d’aprendre a utilitzar-lo. La utilització de GeoGebra té un cost temporal important en l’aprenentatge de les ferramentes i comandaments necessaris.
El curs de GeoGebra té com a objectiu familiaritzar a l’alumnat en un temps molt curt, amb les ferramentes i comandaments, mitjançant una col·lecció d’activitats d’execució ràpida, auto-avaluables, compatibles amb Moodle, de dificultat creixent amb la incorporació progressiva de les ferramentes, que van des la primera amb una sola ferramenta, fins activitats que requereixen la utilització de múltiples ferramentes i comandaments.
Introducció
Una de las dificultats més apreciables en el desenvolupament de les competències matemàtiques del nostre alumnat, és la resolució de problemes amb contingut geomètric. En les competències aritmètiques i algebraiques l’alumnat té instruments, les calculadores aritmètiques i algebraiques, que faciliten la verificació dels càlculs. GeoGebra, no solament pot ocupar un paper similar respecte de la resolució dels problemes geomètrics, és un veritable instrument d’investigació en la docència de primària i secundària.
La introducció de GeoGebra en l’aula de matemàtiques presenta importants dificultats: Primer, l’ensenyament actual no contempla l’ús generalitzat de sistemes informàtics en les aules de matemàtiques les aules d’informàtica estan copades per les assignatures d’informàtica i tecnologia, i la instrumentalització informàtica de l’aula de matemàtiques encara està molt lluny, les aules de matemàtiques, tenen com a molt un ordinador, una pantalla, un projector i uns altaveus, que possibiliten la comunicació del professorat, però no de la investigació en l’aula amb les TIC. Segon, la utilització de GeoGebra requereix també d’una instrumentalització de l’alumnat, GeoGebra pot consumir un temps important en la resolució de problemes i moltes vegades el raonament geomètric pot quedar emmascarat pels procediments d’utilització del programari.
Un curs de GeoGebra per l’alumnat
En el moment que utilitzem GeoGebra (l’artefacte) entre l’alumnat (subjecte) i la resolució de problemes geomètrics (objecte) hem de crear una gènesis instrumental, un procés que transforme el programari de GeoGebra en un veritable instrument que facilite els processos de raonament geomètric (Ruiz, 2011).
Per a poder interaccionar de forma simultània amb tot l’alumnat he creat un curs de GeoGebra en un sistema de gestió de continguts Moodle 3.3 amb el connector de GeoGebra 3.0.
Aquest curs presenta una seqüència d’activitats de GeoGebra d’execució ràpida, autoavaluatives, de dificultat creixent i amb la possibilitat de col·laboració entre l’alumnat mitjançant fòrums.
El curs no intenta ser un manual exhaustiu de la utilització del programari, solament realitzar un recorregut per un petit subconjunt de ferramentes i comandaments de GeoGebra amb la intenció d’adquirir una destresa bàsica en el control dels objectes geomètrics dins del programari, el dibuix de punts, rectes, semirectes, segments, vectors, polígons, circumferències, arcs i transformacions com les translacions, reflexions, inversions i rotacions.
Les activitats són d’execució ràpida, especialment les primeres, amb la intenció de centrar l’activitat en una sola ferramenta i després en la combinació de varies ferramentes i comandaments- L’alumnat amb bones competències matemàtiques i digitals completen el curs en menys de dues hores, repartides en varies sessions curtes, l’alumnat amb més dificultat realitza el curs de forma incompleta entre tres i quatre hores.
He considerat que una experiència d’instrumentalització pot ser avaluada de forma automàtica, a pesar que és la modalitat més pobre en continguts conceptuals (Zapata, 2010), s’adapta molt bé per la necessitat d’immediatesa, per això, totes les activitats són autoavaluables i transfereixen la puntuació al sistema de qualificació de Moodle mitjançant la variable “grade” del programari de GeoGebra, possibilitant que la comunicació de l’alumnat es concentre en els aspectes més dificultosos del curs. L’alumnat no ha utilitzat els fòrums públics de Moodle, per a resoldre les dificultats, prefereix la comunicació amb els companys de forma privada, amb mòbil, i preguntar al professorat a classe quant hi ha unes quantes persones que tenen la mateixa dificultat. Un aspecte important pel professorat en un entorn Moodle és l’observació del temps que necessiten per a realitzar cada activitat.
GeoGebra permet l’ocultació dels diferents elements que conformen la finestra interactiva del programari, i per tant centrar l’atenció de l’alumnat exclusivament en els elements necessaris. La primera activitat solament presenta la ferramenta “mou” i la finestra gràfica, en les següents activitats apareixen les ferramentes noves, però no s’oculten les ferramentes utilitzades en les activitats anteriors, amb la intenció de que l’entorn de GeoGebra siga cada vegada més paregut a l’estat estàndard del programari.
Les activitats
Les activitats estan dividides en cinc blocs: A, primers passos amb GeoGebra, que inclou les activitats més senzilles amb punts i línies. B, activitats amb polígons. C, activitats amb les circumferències i els arcs. D, finalment dediquem un capítol a la simetria, que proporciona unes eines molt interesants per a moltes construccions. E, també hi ha una enquesta final que podeu observar en el segon annex, per a que l’alumnat realitze una petita valoració del curs.
Les imatges de les activitats s’han concentrat en el primer annex amb la intenció d’estalviar espai i facilitar la búsqueda, aprofitant la mateixa codificació que tenen en el curs, observareu l’estat inicial i final de cada activitat.
En el tercer annex apareixen totes les ferramentes, comandaments i zones de la finestra de GeoGebra, utilitzades en el curs. És un petit subconjunt, però molt representatiu com àpat d’entrada a GeoGebra.
Un dels aspectes més reiteratius al llarg del curs és el canvi de nom dels objectes. Hi ha molta costum de deixar a GeoGebra que genere els noms dels objectes geomètrics de forma automàtica i en petites construccions pot ser adequat despreocupar-se d’aquest aspecte, però en la resolució de problemes és més convenient que els objectes tinguen els noms adequats al raonament que estem considerant. Altra raó important de controlar els noms, és l’avaluació automàtica. Cada vegada que l’alumnat interacciona amb l’activitat, afegeix o elimina un objecte o simplement el canvia de nom o el modifica, GeoGebra calcula la puntuació, amb les següents consideracions: El primer grup d’objectes està format per les variables “grade” i “puntuació” que s’utilitzen per a emmagatzemar la qualificació de l’activitat, els objectes inicials de l’activitat que no puntuen, els objectes demanats a l’alumnat sumen en total 10 punts i finalment la resta d’objectes creats per l’alumnat puntuen negativament.
L’avaluació
Les activitats s’avaluen automàticament de 0 a 10 i aquesta nota és transferida al sistema de qualificació de Moole mintjançant la variable “grade” de GeoGebra.
En activitats de GeoGebra hem d’activar l’opció “Activitat de GeoGebra / edita / edita paràmetres / qualificacions / activitat autopuntuable” per acceptar el contingut de la variable “grade”.
Com a nota global no s’ha utilitzat cap paràmetre del curs-moodle, s’ha utilitzat el paràmetre global de moodle situat en “Tauler / Administració del lloc / Qualificacions / Paràmetres de la categoria de qualificació / Agregació” amb el valor “Mitjana de les qualificacions” combinat amb el paràmetre “Tauler / Administració del lloc / Qualificacions / Paràmetres de la categoria de qualificació / Exclou les qualificacions buides” amb el valor “No” imposat, d’aquesta manera el sistema de qualificació calcula la mitjana i avalua amb zero les activitats no realitzades.
Conclusions
Malgrat la pèrdua dels resultats quantitatius per problemes amb el servidor informàtic, sí que és possible arribar a conclusions qualitatives de les converses a classe, ja que és aquest l’entorn preferit per a resoldre les dificultats.
Les tecnologies de la informació i la comunicació són una eina interessant que permet actuar en totes les competències bàsiques, per tant han de formar part de les aules, a l’abast del professorat i de l’alumnat.
La relació acadèmica entre l’alumnat ha millorat, les persones amb menys competències digitals i geomètriques demanen assessorament a les que en tenen més.
Les competències digitals estan molt centrades en el mòbil i molts alumnes solament utilitzen l’ordinador en l’institut, amb aquesta activitat tenen que utilitzar moltes vegades les tabletes i ordinadors dels pares, millorant la competència digital amb aquests instruments.
El taller
El taller que presente en la IV jornada de GeoGebra de la Comunitat Valencia tindrà dues parts, la primera serà una exposició d’uns quinze minuts explicant les característiques fonamentals del curs de GeoGebra per a l’alumnat i una segona part on els assistents rebran la URL del curs de GeoGebra, un nom d’usuari i una clau, per a interaccionar amb el curs i que puguen experimentar la màxima quantitat d’activitats i de forma simultània realitzar les preguntes que consideren oportunes.
El sistema d’autoavaluació. Una mirada a l’interior
El sistema d’avaluació automàtica no és l’objectiu del taller, però pot ser interessant per al professorat que vol crear activitats de GeoGebra i vol incorporar aquesta característica.
Actualment tots els sistemes de programació funcionen amb esdeveniments, i GeoGebra no és una excepció, quan és produeix un esdeveniment, el sistema executa el procediment associat a ell. GeoGebra deixa solament dos esdeveniments disponibles per al creador d’activitats: el canvi de valor d’un objecte i l’acció “clic” del ratolí.
Per sort GeoGebra incorpora el llenguatge JavaScript i l’objecte “ggbApplet” que facilita la comunicació entre els objectes de GeoGebra i el llenguatge de programació JavaScript. És aquest objecte el que ens proporciona una col·lecció més amplia d’esdeveniments que possibilitaran al programador controlar de forma automàtica l’activitat de l’alumnat.
Per explicar el procediment d’avaluació automàtica i les seues possibilitats utilitzaré una construcció d’una recta perpendicular “s” a altra recta “r” que passa per un punt exterior “P”.
En l’estat inicial existiran solament 4 objectes, la variable “grade” que emmagatzema la puntuació, el text “puntuació” que permet observar-la, la recta “r” i el punt “P”.
grade = 0 amb la propietat “Habilita selecció” desactivada.
puntuació = “Puntuació: ” + grade amb la propietat “Habilita selecció” desactivada.
r : 2 y = x + 1 de color roig i gruix 5.
P = (1 , 0 ) de color morat i mida 4.
En la finestra “JavaScrip Global” escriureu les següents funcions de JavaScript, encarregades de l’autoavaluació.
function ggbOnInit() {
ggbApplet.registerAddListener( “ObjecteNou” );
ggbApplet.registerRemoveListener(“ObjecteEsborrat”);
ggbApplet.registerUpdateListener(“ObjecteModificat”);
ggbApplet.registerRenameListener(“ObjecteNombrat”);
}
// Surt la quantitat d’objectes
function QuantitatObjectes(){ return(ggbApplet.getObjectNumber());}
// Entra en número d’objecte i surt el nom
function Nom(Obj){ return(”+ggbApplet.getObjectName(Obj));}
// Entra el nom de l’objecte i surt el tipus
function Tipus(nom){ return(”+ggbApplet.getObjectType(nom));}
// Entra el nom de l’objecte i surt la definició
function Def(nom){ return(”+ggbApplet.getDefinitionString(nom));}
// Entra el nom actual i el nom nou
function Renombra(nom0,nom1){ ggbApplet.renameObject(nom0,nom1);}
// Entra el nom i esborra l’objecte si existeix
function Esborra(nom){ if (ggbApplet.exists(nom)){ggbApplet.deleteObject(nom);};}
// Entra un comandament
function Comandament(text){ ggbApplet.evalCommand(text);}
// Entra nom i el color
function Color(nom,r,g,b){ggbApplet.setColor(nom,r,g,b);}
// Entra nom i el grossor línea
function Grossor(nom,g){ggbApplet.setLineThickness(nom,g);}
// Entra nom i la grandària del punt
function Grandaria(nom,g){ggbApplet.setPointSize(nom,g);}
// Entra nom i el valor
function Valor(nom,v){ggbApplet.setValue(nom,v);}
function ObjecteNou(Obj){
Estudi(Obj);
}
function ObjecteEsborrat(Obj){
if (Obj==”r”) {
Comandament(“r:2y=x+1”);
Color(‘r’,255,0,0);
Grossor(‘r’,5);
};
if (Obj==”P”) {
Comandament(“P=(1,0)”);
Color(‘P’,102,0,153);
Grandaria(‘P’,4);
};
Estudi(Obj);
}
function ObjecteModificat(Obj){
if (Obj != ‘grade’ && Obj != ‘puntuació’){
Estudi(Obj);
}
}
function ObjecteNombrat(Obj0,Obj1){
if (Obj0==’P’) { Renombra(Obj1,’P’) };
if (Obj0==’r’) { Renombra(Obj1,’r’) };
Estudi(Obj0);
}
function Estudi(Obj){
var d1=’Recta que passa per P i és perpendicular a r’;
var t1=’line’;
var n=QuantitatObjectes();
var grade=0;
var i=0;
for (i=0;i<n;i++){
if (Nom(i)!=’grade’ && Nom(i)!=’puntuació’ && Nom(i)!=’r’ && Nom(i)!=’P’){
if (Nom(i)==’s’){
if (Tipus(Nom(i))==t1 && Def(Nom(i))==d1){grade+=10;};
} else {
grade-=0.5;
};
}
};
if (grade<0) {grade=0};
if (grade>10) {grade=10};
Valor(‘grade’,grade);
}
La funció “ggbOnInit” està definida, però originalment buida, és l’encarregada d’executar instruccions abans de la creació de la finestra de GeoGebra, concretament la utilitzareu per associar quatre funcions JavaScript als quatre esdeveniments que pot generar l’alumnat al interaccionar amb l’activitat. Cada vegada que l’alumne cree, esborre, modifique o canvie el nom d’un objecte s’executaran les funcions “ObjecteNou”, “ObjecteEsborrat”, “OnjecteModificat” i “ObjecteNombrat”.
A continuació hi ha una sèrie de funcions JavaScript que solament tenen la intenció de simplificar la utilització de l’objecte “ggbApplet” per a fer més comprensible la programació. “QuantitatObjectes()”, indica la quantitat d’objectes que té la construcció. “Nom(Obj)”, indica el nom de l’objecte a partir del seu número. “Tipus(nom)”, indica el tipus d’objecte en anglès. “Def(nom)”, indica la definició de l’objecte en l’idioma seleccionat, per tant la programació depèn de l’idioma seleccionat. “Renombra(nom0,nom1)”, canvia el nom d’un objecte. “Esborra(nom)”, esborra un objecte. “Comandament(text)”, executa un comandament de GeoGebra. “Color(nom,r,g,b)”, modifica el color d’un objecte. “Grossor(nom,g)”, modifica el grossor d’una línia. “Grandaria(nom,g)”, modifica la grandària d’un punt. “Valor(nom,v)”, modifica el valor d’una variable numèrica.
La funció “ObjecteNou(Obj)” captura la creació d’un objecte nou i executa la funció que estudiarà la puntuació.
La funció “ObjecteEsborrat(Obj)” captura l’acte d’esborrar un objecte i abans de realitzar l’estudi de la puntuació, verifica si l’alumnat ha esborrat els objectes inicials, tornan-los a construir.
La funció “ObjecteModificat(Obj)” actua si un objecte canvia de definició, i com l’estudi de la puntuació modifica els objectes “grade” i “puntuació” entraríem en un bucle sense fi i és per això que queden exclosos de l’esdeveniment.
La funció “ObjecteNombrat(Obj0,Obj1)” captura els canvis de nom, però en el cas que l’alumnat modifique els noms dels objectes inicials, aquests són recuperats
Finalment la funció “Estudi(Obj)” defineix les variables “d1” amb la definició de l’objecte on poseu observar que el text està relacionat amb l’idioma activat en GeoGebra i amb els noms dels objectes, “t1” indica el tipus, sempre en anglès, “n” la quantitat d’objectes, “grade” és una variable de JavaScript que serà transferit a l’objecte de GeoGebra amb el mateix nom. Com podeu observar l’entorn de JavaScript és diferent del sistema de GeoGebra. Amb un bucle realitzem un recorregut del objectes, el objectes “grade”, “puntuació”, “r” i “P” queden exclosos, l’objecte “s” solament puntua si té la definició i el tipus desitjat i la resta d’objectes resten puntuació. Finalment s’acota el valor de la variable “grade” i s’envia el valor a l’objecte “grade” de GeoGebra.
Mes enllà dels comandaments
L’objecte “ggbApplet” ens proporciona un gran conjunt de funcions per a connectar GeoGebra i JavaScript, però incompleta. Per exemple, és possible animar o aturar un objecte, però no és possible detectar el seu estat. Això significa que si l’alumnat activa o desactiva el moviment és impossible detectar automàticament l’acció.
Encara no està tot perdut, l’objecte “ggbApplet” ens permet la lectura, modificació i escriptura del document GeoGebra definit en el llenguatge XML. La idea és capturar el document en una variable de text i buscar l’estat de moviment de l’objecte analitzat.
L’estat de cada objecte de GeoGebra queda definit en el llenguatge XML amb una sèrie d’elements i cada element amb una sèrie d’etiquetes. Per a capturar el valor d’una etiqueta comencem amb la lectura de la definició de l’objecte en XML. Observeu que la funció ggbApplet.getXML(objecte) està concatenada amb un text buit, és un problema que vaig detectar, moltes funcions de JavaScript eren incompatibles amb els textos enviats per GeoGebra, quedant el problema solucionat al afegir prèviament la concatenació d’un text buit.
Mitjançant una expressió regular realitzem una extracció del text tancat entre dobles cometes situat a la dreta del nom de l’element i del nom de l’etiqueta. La funció “test” verifica que l’expressió buscada existeix, la funció “match” transforma totes les expressions trobades en una matriu, solament trobarà una única expressió. Finalment tornem el primer element de la matriu.
La funció “LlegeixAnimable(nom)” busca l’etiqueta “playing” de l’element “animation” de l’objecte indicat i tornarà “true” si té l’animació activada o “false” si està desactivada.
function getOBJ(objecte,element,etiqueta){
var xml=”+ggbApplet.getXML(objecte);
var re= new RegExp (element+’.*’+etiqueta+’=”([^”]*)”‘);
if (re.test(xml)){
var v=xml.match(re);
return v[1];
} else {
return false;
};
}
function LlegeixAnimable(nom){
return(getOBJ(nom,’animation’,’playing’)==’true’);
}
Els problemes en la interacció Moodle-GeoGebra
És pràcticament impossible que al programar un sistema informàtic, aquest contemple totes les situacions en les que serà executat, el connector de GeoGebra per a Moodle no és una excepció. En un document GeoGebra estàndard que controle la variable “grade” com element de transmissió de la puntuació a Moodle no observarem cap problema. Si instal·lem una activitat amb qualsevol del documents utilitzats, tampoc. Però existeix una situació comprometida degut a les particularitats d’aquests documents de GeoGebra en les restauracions dels cursos. Aquests documents tenen una part important del seu programari escrit en JavaScript, responsable de la variable “grade” i aquest queda desactivat en les restauracions dels cursos.
La solució és prou senzilla, mentre esperem alguna nova versió amb el problema corregit, una vegada es fa la restauració del curs amb la intenció de duplicar-lo, hem d’activar l’edició i recórrer totes les activitats de GeoGebra i simplement editar-les i guardar-les una per una, per activar el codi JavaScript de cada activitat.
Bibliografia
Couchoud Pérez, J. M. (2017). Curs de GeoGebra. Recuperat de https://www.geogebra.org/m/rpN4xDde
IGInstitute (2017), Referencia: JavaScript. International GeoGebra Institute. Recuperat de https://www.geogebra.org/manual/es/Referencia:JavaScript
Ruiz López, N. (2011). Resolución de problemas geométricos con GeoGebra en la formación de profesorado de educación primaria: un estudio de casos. 1ª Conferéncia Latino Americana de GeoGebra. ISSN 2237-9657, pp.51-64. Recuperado de
https://revistas.pucsp.br/index.php/IGISP/article/viewFile/8607/6577
Zapata Ros, M. (2010). Evaluación de competencias en entornos virtuales de aprendizaje y docencia universitaria. RED, Revista de Educación a Distancia. Sección de Docencia Universitaria en la Sociedad del Conocimiento . Nº 1. Recuperado de
https://www.um.es/ead/reddusc/1/eval_compet.pdf
Imatges
Les imatges de les ferramentes estan copiades de l’editor de llibres de GeoGebra.
Els mapes de Tabarca i de Central Park estan copiats de Google Earth
Arc de ferradura. Recuperat de
http://elmundoderafalillo.blogspot.com.es/2016/02/arcos-de-malaga-de-herradura-por-arcos.html
El dofí. Recuperat de http://www.pngpix.com/download/dolphin-png-image-2
El gat. Recuperat de http://www.chismesmundo.com/queridas-mascotas-los-gatos/
Les empremtes. Recuperat de http://www.flaticon.es/icono-gratis/huella-de-pie_1275
El símbol de GeoGebra. Recuperat de http://www.relpe.org/club-geogebra-iberoamericano/
La doble G. Recuperat de https://pixabay.com/es/carta-g-may%C3%BAscula-alfabeto-abc-146001/
El deu. Recuperat de https://es.dreamstime.com/fotos-de-archivo-libres-de-regal%C3%ADas-n%C3%BAmero-enmarcado-de-oro-10-image3052248
El tigre. Recuperat de http://chameleons.com.ua/fotooboi/1291–.html
La flor. Pilar Moreno. Recuperat de http://jmora7.com/Mosaicos/index.html
Les demés imatges estan copiades dels “applets” de GeoGebra construïts per l’autor.
Annex I. Estat inicial i final de les activitat del curs de GeoGebra.
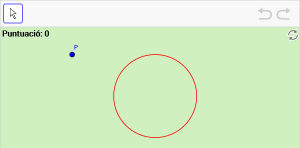
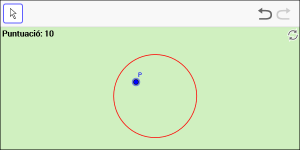
A1. Mou el punt
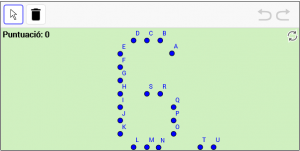

A2. Esborreu els punts


A3. Dibuixeu un punt anomenat “P”

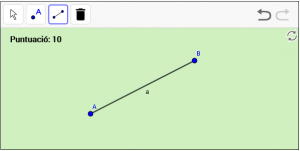
A4. Dibuixeu un segment anomenat “a”
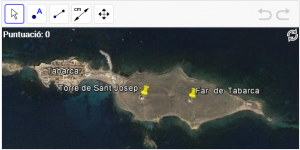
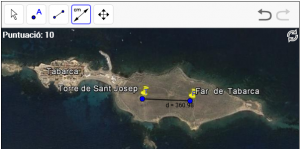
A5. Calculeu la distància des de la torre de Sant Josep fins el far de Tabarca
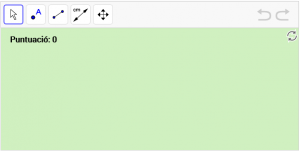
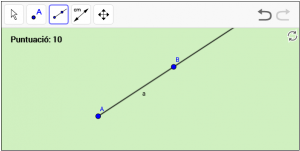
A6. Dibuixeu una semirecta anomenada “a”
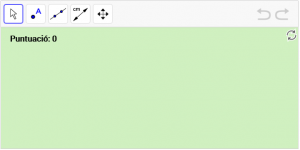
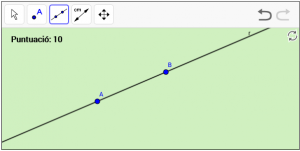
A7. Dibuixeu una recta anomenada “r”
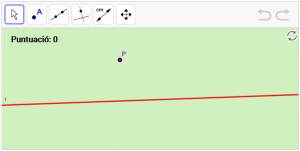
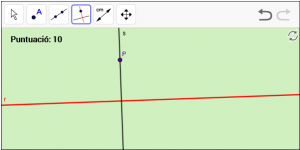
A8. Dibuixa una recta anomenada “s” perpendicular a la recta r que passe pel punt “P”
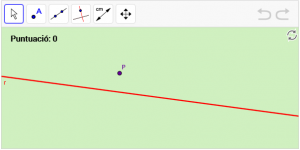
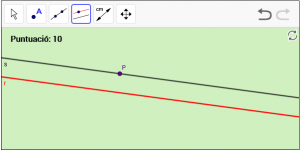
A9. Dibuixa una recta anomenada “s” paral·lela a la recta r que passa pel punt “P”
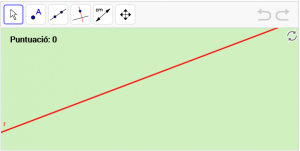
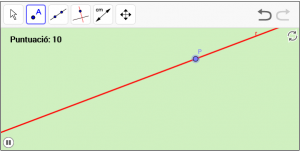
A10. Dibuixeu un punt “P” que viatge per la recta “r”
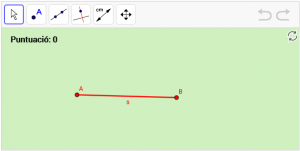
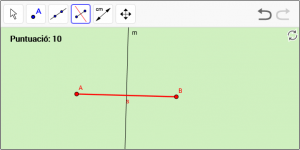
A11. Dibuixeu la mediatriu “m” del segment “s”
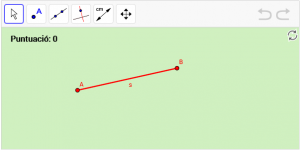
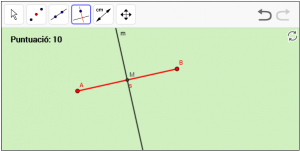
A12. La mediatriu és la recta perpendicular a un segment que passa pel seu punt mitjà
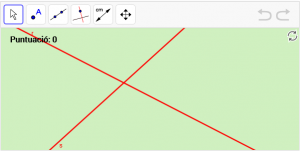
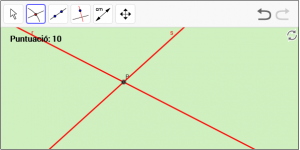
A13. Dibuixeu la intersecció de dues rectes secants
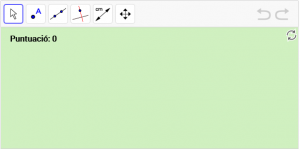
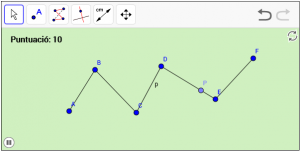
A14. Dibuixeu un punt “P” dinàmic en una línia poligonal “p”
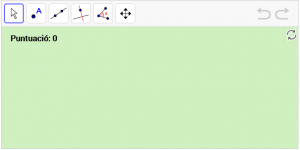
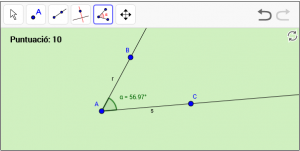
A15. Dibuixeu un angle agut anomenat alfa “α”
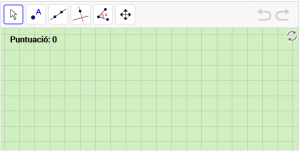
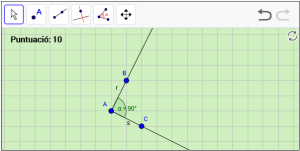
A16. Dibuixeu un angle recte anomenat “α”
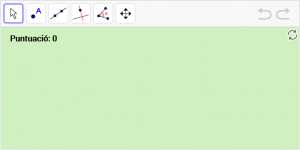
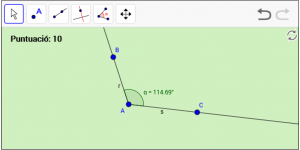
A17. Dibuixeu un angle obtús anomenat “α”
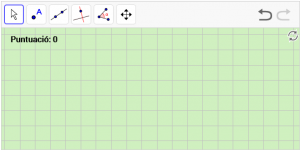
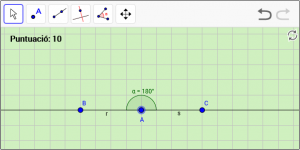
A18. Dibuixeu un angle pla anomenat “α”
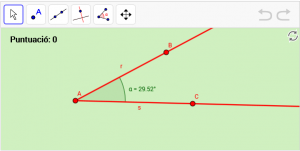
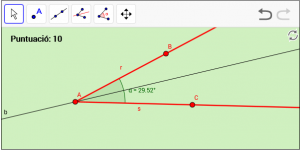
A19. Dibuixeu la bisectriu “b” de l’angle “α”
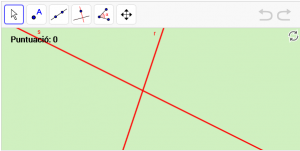
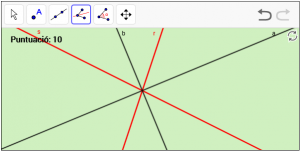
A20. Dibuixeu la bisectriu de dues rectes secants
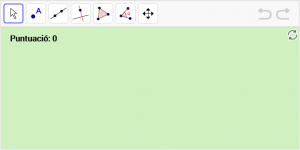
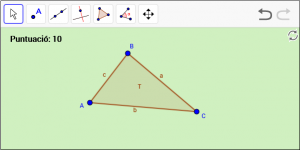
B1. Dibuixeu un triangle anomenat “T”
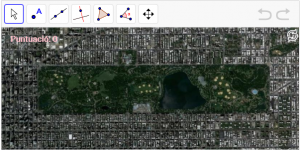
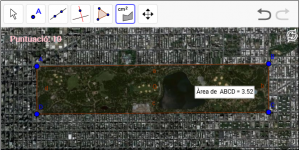
B2. Calculeu l’àrea en km² de CENTRAL PARK situat en Manhattan (New York)
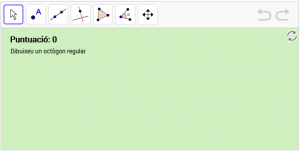
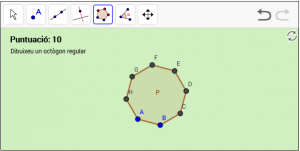
B3. Dibuixeu el polígon regular en l’àrea gràfica
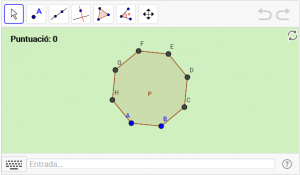
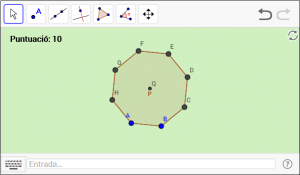
B4. Dibuixeu el punt central d’un polígon regular
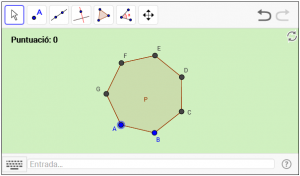
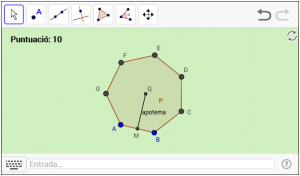
B5. Dibuixeu l’apotema d’un polígon regular
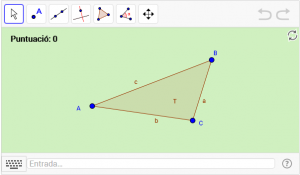
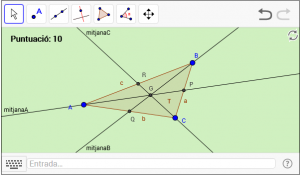
B6. Dibuixeu el baricentre d’un triangle
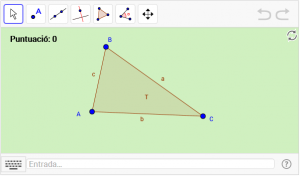
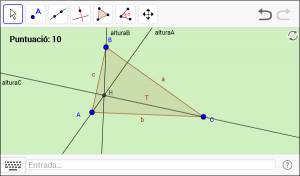
B7. Dibuixeu l’ortocentre d’un triangle
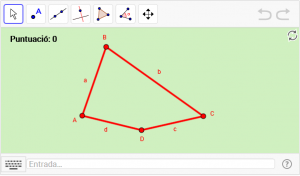
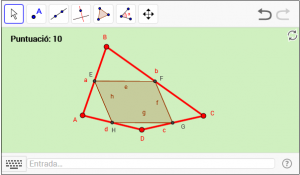
B8. Un teorema amb paral·lelograms
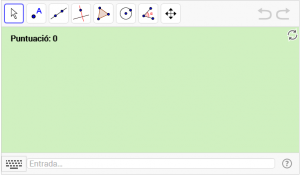
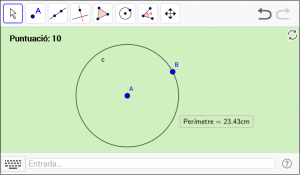
C1. Dibuixeu una circumferència i calculeu el perímetre
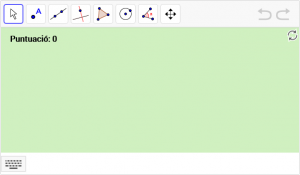
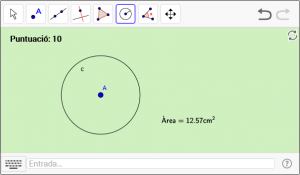
C2. Dibuixeu una circumferència centrada en el punt A amb 2 unitats de radi
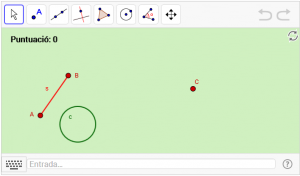
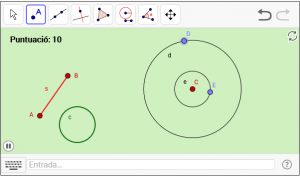
C3. Dibuixeu dues circumferències
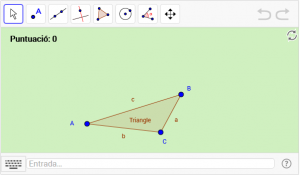
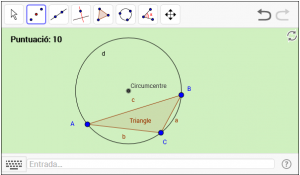
C4. Dibuixeu el circumcentre del triangle
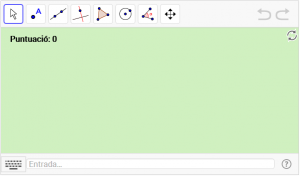
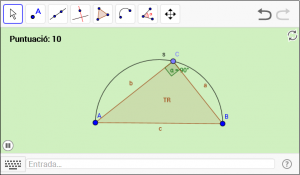
C5. Dibuixeu un triangle inscrit en una semicircumferència
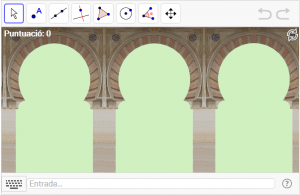
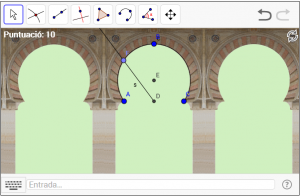
C6. Dibuixeu l’arc de ferradura
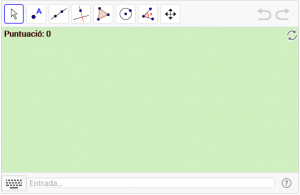
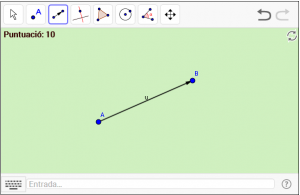
D1. Dibuixeu un vector
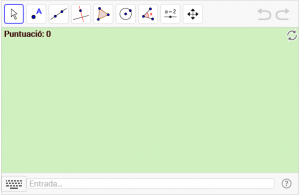
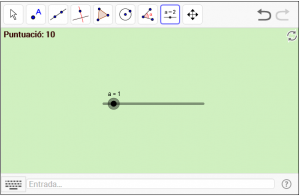
D2. Prepareu un punt lliscant
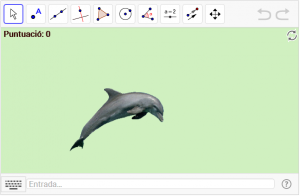
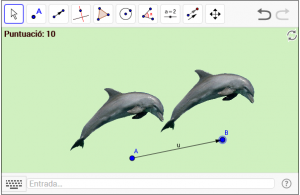
D3. Traslladeu el dofí amb un vector
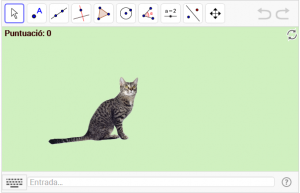
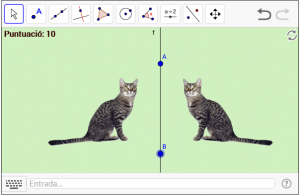
D4. Reflectiu el gat respecte d’un eix
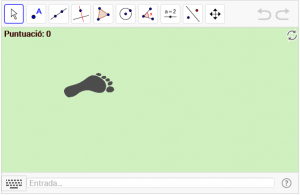
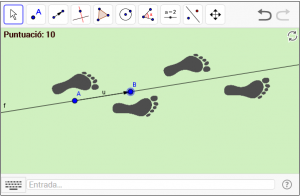
D5. Busqueu empremtes
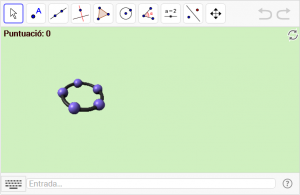
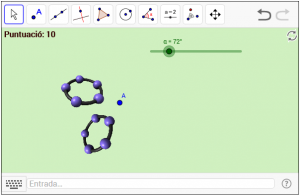
D6. Gireu el símbol de GeoGebra

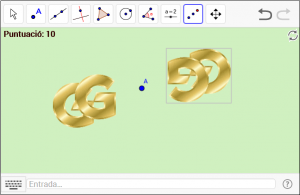
D7. Gireu el símbol de GeoGebra 180º
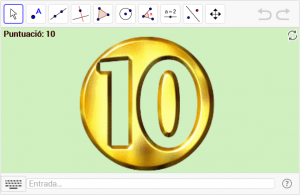

D8. Per entendre la simetria identitat no cal fer res
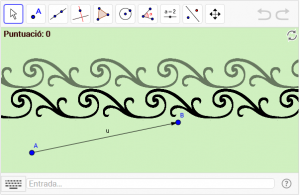
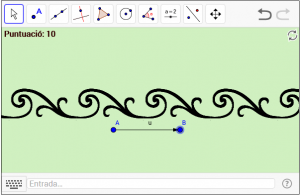
D9. La simetria de translació dels frisos
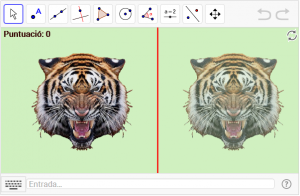
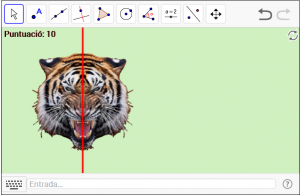
D10. El tigre simètric
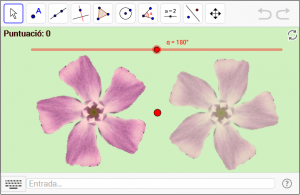
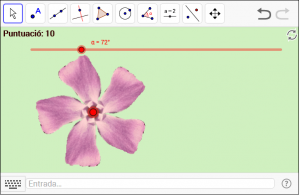
D11. La flor simètrica
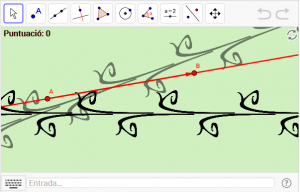
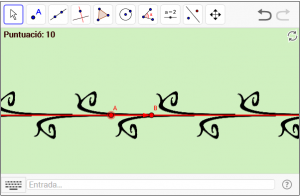
D12. Frisos amb lliscament
Annex II. Enquesta
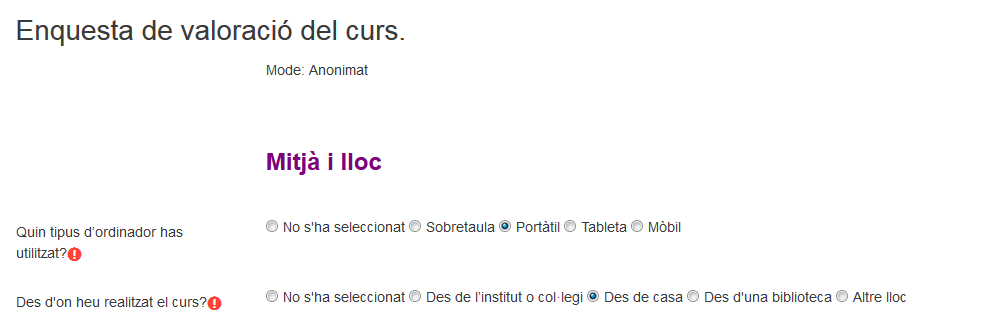
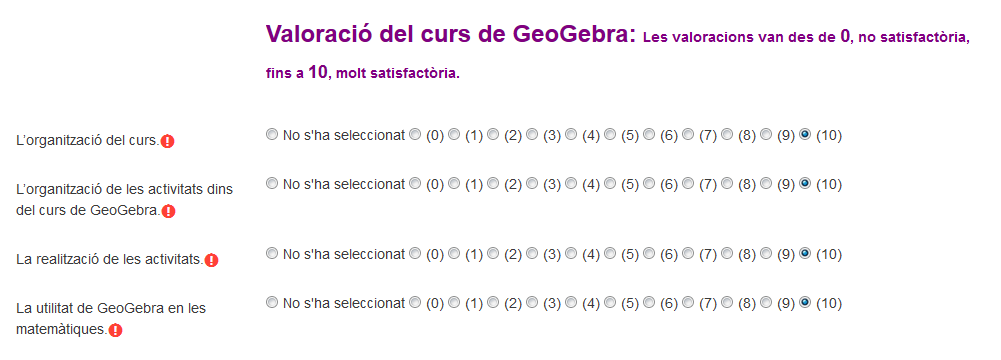
Annex III. Primera aparició de les ferramentes i comandaments utilitzats en el curs.
| Utilitat | Tipus | Activitat | Icona |
| Agrupació de ferramentes | A5 | ||
| Allunya | Ferramenta | A5 | |
| Animació activada | Menú contextual | A10 | |
| Angle | Ferramenta | A15 | |
| Apropa | Ferramenta | A5 | |
| Arc de circumferència que passa per tres punts | Ferramenta | C6 | |
| Àrea | Ferramenta | B2 | |
| Bisectriu | Ferramenta | A19 | |
| Canvi de nom | Menú contextual | A3 | |
| Circumferència amb centre i que passe per un punt | Ferramenta | C1 | |
| Circumferència donats centre i radi | Ferramenta | C2 | |
| Circumferència que passa per tres punts | Ferramenta | C4 | |
| Centroide | Comandament | B4 | |
| Compàs | Ferramenta | C3 | |
| Composició de comandaments | D5 | ||
| Desplaçament de la finestra gràfica | Ferramenta | A5 | |
| Esborra | Ferramenta | A2 | |
| Gir al voltant d’un punt | Ferramenta | D6 | |
| Graella | A16 | ||
| Intersecció | Ferramenta | A13 | |
| Intersecció | Comandament | B6 | |
| Línia poligonal | Ferramenta | A14 | |
| Longitud | Ferramenta | A5 | |
| Mediatriu | Ferramenta | A11 | |
| Mou | Ferramenta | A1 | |
| Perpendicular | Comandament | B7 | |
| Polígon | Ferramenta | B1 | |
| Polígon | Comandament | B8 | |
| Polígon regular | Ferramenta | B3 | |
| Punt | Ferramenta | A3 | |
| Punt lliscant | Ferramenta | D2 | |
| Punt mitjà o centre | Ferramenta | A12 | |
| PuntMitjà | Comandament | B5 | |
| Recta | Ferramenta | A7 | |
| Recta | Comandament | B5 | |
| Recta paral·lela | Ferramenta | A9 | |
| Recta perpendicular | Ferramenta | A8 | |
| Segment | Ferramenta | A4 | |
| Segment | Comandament | B5 | |
| Semicircumferència | Ferramenta | C5 | |
| Semirecta | Ferramenta | A6 | |
| Simetria | Comandament | D5 | |
| Simetria central | Ferramenta | D7 | |
| TextFórmula | Comandament | C1 | |
| Translació | Comandament | D5 | |
| Translació segons un vector | Ferramenta | D3 | |
| Vector entre dos punts | Ferramenta | D1 | |
| Zona d’entrada de comandaments | B4 | ||
| Zona de ferramentes | A1 | ||
| Zona gràfica | A1 |
Deixa un comentari