Matemàtiques 0.1 fins l'infinit

Construcció de l’applet “Experimentant amb quadrilàters i el teorema de Pick”

Modalitat: Taler presentat en les XII Jornades d’Educació Matemàtica de la Comunitat Valenciana “Matemàtiques per entendre el món”. València a 30 de setembre i 1 d’octubre de 2016.

Nivell educatiu: primària i secundària

Paraules clau: GeoGebra, quadrilàters, Pick, geometria, interactiva

Resum

Aquest taller presenta l’applet de GeoGebra anomenat “Experimentant amb quadrilàters i el teorema de Pick” (Couchoud 2016). S’ha treballat en l’optativa instrumental de matemàtiques de 1r d’ESO amb alumnat amb baixes competències de geometria. Permet realitzar activitats molt variades amb quadrilàters de forma interactiva, des de l’estudi dels noms, anàlisi de les propietats, fins l’estudi de les àrees amb el teorema de Pick. Distingeix els quadrilàters simples de la resta de quadrilàters per evitar confusions a l’alumnat. Els colors són una eina important per a la identificació de les propietats: costats iguals, angles iguals, diagonals iguals. En el taller, s’ensenyaran les estratègies principals de la construcció, molt interessants per l’aplicació en altres construccions amb GeoGebra.

Introducció

Els quadrilàters són una de les famílies poligonals més utilitzades en la societat, tant en les expressions tecnològiques com artístiques, i formen part dels continguts curriculars de primària i secundària.

Les múltiples possibilitats de treball que permet aquest applet fan que connecte directament amb moltes competències (Ministeri d’Educació, Cultura i Esport. MECE 2015). Amb l’ús de quadrilàters, la competència matemàtica que destaca és la geomètrica; amb el càlcul d’àrees, la competència aritmètica; amb el programa GeoGebra, la competència digital; amb el treball en equip, es desenvolupen la competència lingüística, la social i el sentit de la iniciativa; la curiositat i la facilitat de participar en un entorn reduït milloren molt la competència d’aprendre a aprendre.

Descripció de l’applet

L’applet presenta un quadrilàter (figura 1) que podeu controlar arrossegant els vèrtexs amb el ratolí, podeu centrar-lo amb el botó de la pantalla “Centra”, augmentar i reduir la grandària dels polígons amb els botons “+” i “-“. Els vèrtexs solament poden viatjar pels encreuats de la graella per a facilitar la construcció dels quadrilàters, l’aplicació del teorema de Pick i, sobretot, facilitar el dibuix en els fulls quadriculats. Quan el quadrilàter no és simple, es torna de color negre.

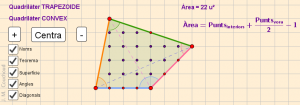
Figura 1

Les caselles de control són les responsables d’adaptar l’applet a l’activitat desenvolupada, per a minimitzar els elements visibles. La casella de control “Nom” permet ocultar i visualitzar el nom i la concavitat o convexitat del quadrilàter; la casella de control “Teorema de Pick” permet ocultar el punts interiors i de la vora del quadrilàter junt a la fórmula, els vèrtexs sempre són visibles; la casella de control “Àrea” permet ocultar i visualitzar l’àrea, la casella de control “Angles” permet ocultar i visualitzar els angles interiors i la casella de control “Diagonals” permet ocultar i visualitzar les diagonals.

Els colors són una part importantíssima en l’anàlisi de les propietats dels quadrilàters. Els costats del mateix color tenen la mateixa longitud, els angles del mateix color són iguals, les diagonals del mateix color són de la mateixa longitud, les diagonals perpendiculars són més gruixudes i els punts d’encreuament de la graella, interiors al polígon són d’un color i els de la vora, del mateix color que els vèrtexs.

L’applet és essencialment interactiu, permet treballar amb un gran grup i solament un ordinador connectat a un projector o en petits grups i un ordinador per equip; l’alumnat treballa les activitats amb folis quadriculats amb quadrats d’un centímetre (figura 1?), els quadrats més petits generen dificultats importants amb l’alumnat amb baixes competències geomètriques. Els tipus d’activitats són molt variades:

1.- Troba i dibuixa en el full tres polígons convexos i tres còncaus (activa solament la casella de control “Nom”).

2.- Representa quadrilàters còncaus i convexos per trobar la característica que els distingeix (activa solament les caselles de control “Nom” i “Angles”).

3.- Troba quadrilàters de nom diferent, dibuixa un de cada. Quantes classes de quadrilàters hi ha? (activa solament la casella de control “Nom”).

4.- Ara que ja recordes totes les classes de quadrilàters, identifica la família dels paral·lelograms, els que tenen dues parelles de costats paral·lels (activa solament la casella de control “Nom”).

5.- Investiga quins quadrilàters tenen sempre les diagonals perpendiculars (activa solament les caselles de control “Nom” i “Diagonals”).

6.- Representa i dibuixa quadrilàters diferents, però petits i calcula l’àrea amb el teorema de Pick. Verifica que el resultat és idèntic al de la pantalla (activa solament les caselles de control “Teorema de Pick” i “Àrea”).

També es poden intercalar activitats orals en forma de joc, sense paper, molt adequades per a l’alumnat amb dificultats en competències lingüístiques.

7.- El professor representa un quadrilàter i l’alumnat identifica el nom i les propietats (activa solament les caselles de control “Angles” i “Diagonals”).

La construcció de l’applet té moltes parts interessants que poden ser aplicades en la construcció d’altres documents de GeoGebra; a continuació teniu un manual complet. Ara desenvolupareu en el taller unes poques parts per facilitar l’autonomia necessària perquè pugueu reconstruir l’applet o reutilitzar les seues parts en altres. Podem destacar la manipulació d’objectes geomètrics en una graella, la identificació del nom d’objectes geomètrics amb unes poques propietats, la visualització d’angles interns independentment de la situació dels vèrtexs, la representació dels punts del teorema de Pick mitjançant llistes, el control de visualització d’objectes i també el control de colors dinàmics amb JavaScript.

Construcció

Engegueu l’ordinador i activeu una finestra de GeoGebra, guardeu-la en la vostra carpeta de treball amb el nom “quadrilàters i el teorema de Pick.ggb”. No oblideu de guardar el document cada pocs minuts de treball. La relació de sentències que podeu utilitzar la trobareu en la web GeoGebra (IGI 2016a, 2016b).

1.- Preparació de l’escenari

Per a facilitar el disseny, recomane la separació de la finestra algebraica que serà ocultada al final de la construcció (Figura 2).

[Cliqueu el símbol “mostra una finestra nova” que apareix al situar el cursor en la capçalera de la finestra algebraica]

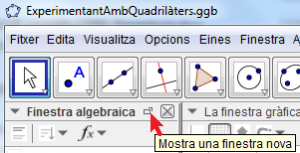
Figura 2

En la finestra de preferències, definireu la majoria de les característiques de la finestra gràfica; podeu entrar directament clicant en el teclat [Ctrl E]. L’objectiu és aconseguir una graella amb quadrats d’una unitat d’àrea independentment de la visualització i que el cursor viatge pels encreuaments.

En la solapa “Bàsic” clicareu el cadenat per fixar la relació 1:1 entre els eixos i modificareu el color del fons, per un altre molt clar.

En la solapa “EixX” desactiveu l’opció “Mostrar l’eix de les x”.

En la solapa “EixY” desactiveu també l’opció “Mostrar l’eix de les y”.

En la solapa “Graella” activeu les opcions “Mostrar quadrícula” i “Distància” amb valors unitat per a la “x” i la “y”.

En la capçalera de la finestra gràfica, observareu un dibuix en forma d’ imant (Figura 3) anomenat “Fixa l’estil de captura de punts” i seleccioneu l’opció “Fixats a la quadrícula”. He observat que aquesta opció es desactiva algunes vegades durant el disseny del programa, però mai en l’execució, solament heu d’activar una altra vegada l’opció “Fixats a la quadrícula” abans de guardar el treball.

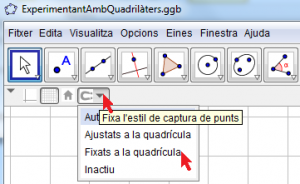
Figura 3

2.- Preparació del quadrilàter

Amb GeoGebra, podeu executar accions amb el menú, amb la barra de ferramentes i amb la casella anomenada “Entrada”; en aquest document donaré prioritat a les instruccions escrites en “Entrada”.

Prepareu els quatre punts, els quatre costats, les diagonals i l’àrea del quadrilàter (Figura 4). No utilitzareu la ferramenta “Polígon” per a mantenir les propietats d’ocultació i de colors independents. L’àrea la definireu amb un polígon dins d’una llista per evitar la duplicació dels elements que formen el quadrilàter.

A=(0,0)

B=(0,1)

C=(1,1)

D=(1,0)

a=Segment[A,B]

b=Segment[B,C]

c=Segment[C,D]

d=Segment[D,A]

d_1=Segment[A,C]

d_2=Segment[B,D]

Q = {Polígon[A, B, C, D]}

Entreu en la finestra de preferències i modifiqueu les propietats dels objectes definits.

Seleccioneu els quatre punts, en la solapa “Color” seleccioneu el roig que és molt cridaner en les projeccions.

Seleccioneu els quatre costats, en la solapa “Bàsic” desactiveu l’opció “Mostra etiqueta” i en la solapa “Estil” definiu un gruix de línia de 7 unitats perquè destaquen els costats del quadrilàter.

Seleccioneu les dos diagonals, en la solapa “Bàsic” desactiveu també l’opció “Mostra etiqueta” i en la solapa “Estil” definiu el gruix de línia d’una unitat i l’estil de línia amb ratlletes.

Seleccioneu la llista “Q”, en la solapa “Bàsic” desactiveu també l’opció “Mostra etiqueta” i en la solapa “Estil” definiu un gruix de línia de zero unitats, solament interessa l’àrea.

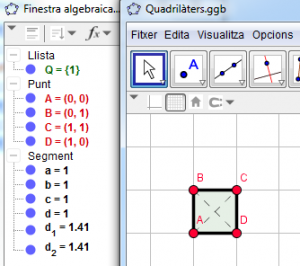
Figura 4

També he observat que els punts, en certes circumstàncies, queden immòbils; a la finestra de preferències, seleccioneu els quatre vèrtexs i en la solapa “Bàsic” desactiveu l’opció “Fixa objecte” abans de guardar el document.

3.- Identificació de quadrilàters simples

Hi ha moltes maneres d’identificar els quadrilàters simples; en aquesta ocasió aprofitareu un parell de característiques, la primera consisteix a identificar l’existència de tres vèrtexs consecutius alineats o coincidents, calculant l’àrea del triangle que formen i l’altra, molt curiosa, per l’existència de les interseccions dels costats oposats, com a indicadors de l’encreuament de costats. En GeoGebra un punt és igual a ell mateix solament si està definit, si un punt passa a l’estat de “no definit” deixa de ser igual a ell mateix.

i_1 = Intersecció[a, c]

i_2 = Intersecció[b, d]

QuadrilàterSimple = (Àrea[A, B, C] > 0) ∧ (Àrea[B, C, D] > 0) ∧ (Àrea[C, D, A] > 0) ∧ (Àrea[D, A, B] > 0) ∧ (¬(i_1 ≟ i_1)) ∧ (¬(i_2 ≟ i_2))

Els punts de les interseccions no són visibles per estar en l’estat “no definit”, però com que no volem observar-los mai, en las finestra de preferències, en la solapa “Bàsic” desactivareu l’opció “Mostrar objecte”.

Els caràcters que no estan en el teclat poden seleccionar-se de la finestreta d’ampliació del teclat (Figura 5).

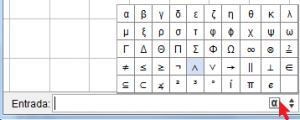
Figura 5

Podeu desplaçar els vèrtexs a situacions on el quadrilàter no és simple i la variable booleana QuadrilàterSimple passarà a valdre false.

4.- Identificació dels quadrilàters còncaus i convexos

Amb l’existència de la intersecció de les diagonals i la variable QuadrilàterSimple serà molt fàcil de distingir la concavitat i la convexitat dels quadrilàters.

i_0 = Intersecció[d_1, d_2]

Convex = QuadrilàterSimple ∧ i_0 ≟ i_0

Còncau = QuadrilàterSimple ∧ (¬(i_0 ≟ i_0))

El punt d’intersecció no ha de ser visible, en las finestra de preferències, en la solapa “Bàsic” desactivareu l’opció “Mostrar objecte”.

5.- Angles interiors

El sistema que utilitza GeoGebra per a definir els angles no permet distingir entre angles interns i externs a un polígon; si dibuixeu els quatre angles interiors i desplaceu els vèrtexs invertint l’ordre de col·locació, passen a ser angles exteriors. L’estratègia consisteix en definir tres famílies d’angles, les dues primeres podran ser o interiors o exteriors i la tercera serà sempre igual a la família que siga interior. Les lletres gregues les podeu trobar en la finestreta d’ampliació del teclat (Figura 5). Podríem prescindir de la tercera família, però aquesta estratègica utilitzada simplificarà moltíssim l’assignació de colors.

α_0 = Angle[D, A, B]

β_0 = Angle[A, B, C]

γ_0 = Angle[B, C, D]

δ_0 = Angle[C, D, A]

α_1 = Angle[B, A, D]

β_1 = Angle[C, B, A]

γ_1 = Angle[D, C, B]

δ_1 = Angle[A, D, C]

α = Si[α_0 + β_0 + γ_0 + δ_0 ≟ 360°, α_0, α_1]

β = Si[α_0 + β_0 + γ_0 + δ_0 ≟ 360°, β_0, β_1]

γ = Si[α_0 + β_0 + γ_0 + δ_0 ≟ 360°, γ_0, γ_1]

δ = Si[α_0 + β_0 + γ_0 + δ_0 ≟ 360°, δ_0, δ_1]

En la finestra de preferències seleccioneu el primers 8 angles i en la solapa “Bàsic” desactiveu l’opció “Mostra objecte”.

Seleccioneu els últims 4 objectes i en la solapa “Bàsic” activeu l’opció “Mostra objecte” i desactiveu “Mostra etiqueta”.

Verifiqueu que sempre apareixen els angles interiors per als quadrilàters simples, més tard ocultareu els angles per a quadrilàters no simples.

6.- Classificació dels quadrilàters

Primer calculareu, amb una variable numèrica, la quantitat de parelles de costats paral·lels amb la suma de dues sentències condicionals; no oblideu d’utilitzar la finestreta d’ampliació del teclat (Figura 5) per a utilitzar el símbol de paral·lelisme.

Paral·leles = Si[a ∥ c, 1, 0] + Si[b ∥ d, 1, 0]

També podeu determinar la perpendicularitat de les diagonals

DiagonalsPerpendiculars = d_1 ⊥ d_2

Per a classificar els quadrilàters, podeu utilitzar moltes condicions diferents, però en totes ha de participar la variable booleana QuadrilàterSimple.

El quadrat

Quadrat = QuadrilàterSimple ∧ Paral·leles ≟ 2 ∧ α ≟ 90° ∧ a ≟ b

El rectangle

Rectangle = QuadrilàterSimple ∧ Paral·leles ≟ 2 ∧ α ≟ 90° ∧ (a ≠ b)

El rombe

Rombe = QuadrilàterSimple ∧ Paral·leles ≟ 2 ∧ (α ≠ 90°) ∧ a ≟ b

El romboide

Romboide = QuadrilàterSimple ∧ Paral·leles ≟ 2 ∧ (α ≠ 90°) ∧ (a ≠ b)

El trapezi rectangle

TrapeziRectangle = QuadrilàterSimple ∧ Paral·leles ≟ 1 ∧ (α ≟ 90° ∧ β ≟ 90° ∨ β ≟ 90° ∧ γ ≟ 90° ∨ γ ≟ 90° ∧ δ ≟ 90° ∨ δ ≟ 90° ∧ α ≟ 90°)

El trapezi isòsceles

TrapeziIsòsceles = QuadrilàterSimple ∧ Paral·leles ≟ 1 ∧ (α ≠ 90°) ∧ (α ≟ β ∧ γ ≟ δ ∨ δ ≟ α ∧ β ≟ γ)

El trapezi escalè

TrapeziEscalè = QuadrilàterSimple ∧ Paral·leles ≟ 1 ∧ (α ≠ β) ∧ (α ≠ γ) ∧ (α ≠ δ) ∧ (β ≠ γ) ∧ (β ≠ δ) ∧ (γ ≠ δ)

El cometa

Cometa = QuadrilàterSimple ∧ Paral·leles ≟ 0 ∧ (a ≟ b ∧ c ≟ d ∨ b ≟ c ∧ d ≟ a)

El trapezoide

Trapezoide = QuadrilàterSimple ∧ Paral·leles ≟ 0 ∧ (¬Cometa)

7.- Els punts de la vora i interiors del quadrilàter

Si tenim una graella amb cel·les en forma de paral·lelogram i un polígon amb els vèrtex situats en els encreuaments de la graella podem utilitzar el teorema de Pick per a calcular l’àrea del polígon. La unitat d’àrea és l’àrea de la cel·la.

$\text{\`Area}=\text{Punts}_{\text{interiors}}+\frac{\text{Punts}_{\text{vora}}}{2}-1$

En aquest document utilitzareu la graella amb cel·les quadrades d’àrea u (Motormuis 2014).

Preparareu una llista de tots els punts situats entre el vèrtex de l’esquerra i el de la dreta i el vèrtexs inferior i superior. Utilitzareu la sentència Seqüència dins d’altra generant una llista de llistes que unificareu amb la sentència Aplana; si no hi ha un quadrilàter simple, genera una llista buida. Aquesta llista ha de ser invisible.

Punts = Si[QuadrilàterSimple, Aplana[Seqüència[Seqüència[(i, j), j, Mín[{y(A), y(B), y(C), y(D)}], Màx[{y(A), y(B), y(C), y(D)}]], i, Mín[{x(A), x(B), x(C), x(D)}], Màx[{x(A), x(B), x(C), x(D)}]]], {}]

Després seleccionareu els punts de la vora amb una estratègia molt interessant, verificant els punts que pertanyen a la línia poligonal entre el primer vèrtex i l’últim; necessitareu un polígon d’àrea nul·la format solament pels costats. El color ha de ser el mateix que el dels vèrtexs, i la mida del punt de tres unitats. Podeu calcular la quantitat de punts amb la instrucció Longitud que compta els elements que hi ha en una llista.

PuntsVora = TriaSi[PuntPertanyRegió[Z, Polígon[{A, B, C, D, A, D, C, B }]], Z, Punts]

P_V = Longitud[PuntsVora]

El punts interiors es poden calcular imposant la condició de ser del polígon però no de la vora, el color ha de ser diferent i la mida del punt de tres unitats. També els heu de comptar.

PuntsInteriors = TriaSi[PuntPertanyRegió[Z, Polígon[{A, B, C, D}]] ∧ (¬PuntPertanyRegió[Z, Polígon[{A, B, C, D, A, D, C, B }]]), Z, Punts]

P_I = Longitud[PuntsInteriors]

Si calculeu el teorema de Pick, trobareu la grata sorpresa que dóna el mateix resultat que hi ha dins de la llista Q.

Pick=P_I+P_V/2-1

8.- Textos

Una vegada heu desenvolupat la part geomètrica, passareu als altres elements que possibiliten la interacció amb l’alumnat. Necessitareu un text que informe del nom del quadrilàter

TextNom = Si[QuadrilàterSimple, “Quadrilàter ” + (Si[Quadrat, “QUADRAT”, “”]) + (Si[Rectangle, “RECTANGLE”, “”]) + (Si[Rombe, “ROMBE”, “”]) + (Si[Romboide, “ROMBOIDE”, “”]) + (Si[TrapeziEscalè, “TRAPEZI ESCALÈ”, “”]) + (Si[TrapeziIsòsceles, “TRAPEZI ISÒSCELES”, “”]) + (Si[TrapeziRectangle, “TRAPEZI RECTANGLE”, “”]) + (Si[Cometa, “COMETA”, “”]) + (Si[Trapezoide, “TRAPEZOIDE”, “”]), “No és un quadrilàter simple”]

Altre que informe de la concavitat o convexitat.

TextConcavitat = Si[QuadrilàterSimple, “Quadrilàter ” + (Si[Còncau, “CÒNCAU”, “”]) + (Si[Convex, “CONVEX”, “”]), “”]

Un tercer text que informe de l’àrea.

TextÀrea = Si[QuadrilàterSimple, “Àrea = ” + Pick + ” u²”, “”]

I, finalment, un text amb la fórmula de Pick en format LaTeX per recordar-la.

TextTeoremaPick = “Àrea=Punts_{interiors}+\frac{Punts_{vora}}{2}-1”

Els textos han de ser cridaners i sobretot visibles en una projecció des de l’última taula de l’aula. Al treballar amb l’activitat no s’han de desplaçar i per això heu de configurar les propietats següents per a garantir el correcte funcionament del document.

Distribuireu els textos en finestra gràfica de forma adequada (Figura 6) i, en la finestra de preferències, seleccionareu els quatre textos. En la solapa “Text” utilitzareu la grandària de lletra “Mitjà” i activareu la lletra negreta. En la solapa “Color” podeu seleccionar el morat o altre que vos agrade. En la solapa “Posició” activareu l’opció “Posició absoluta en pantalla” per a independitzar la posició del text de la graella. I finalment en la solapa “Bàsic” activareu la propietat “Mostra objecte” per a impedir que l’usuari puga modificar la posició dels textos.

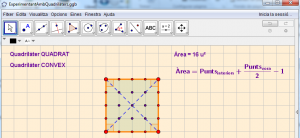
Figura 6

9.- Botons

Una de les eines principals per a controlar qualsevol programa són els botons; en el nostre cas els utilitzarem per a controlar la grandària de la graella i el centrat de la figura en la finestra gràfica.

Utilitzeu la barra de ferramentes, activeu la ferramenta botó i cliqueu en la posició que desitgeu situar-lo. Escriviu el signe “+” en la llegenda i la sentència Apropa[1.2] i cliqueu el botó “D’acord” (Figura 7).

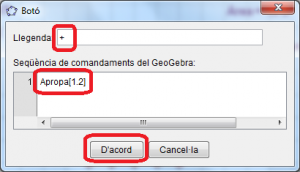
Figura 7

En el segon botó escriviu “Centra” en la llegenda, la sentència CentreFinestra[(A+B+C+D)/4] i cliqueu el botó “D’acord” (Figura 8).

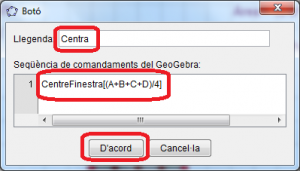
Figura 8

En el tercer botó escriviu “-“ en la llegenda, la sentència Allunya[1.2] i cliqueu el botó “D’acord” (Figura 9).

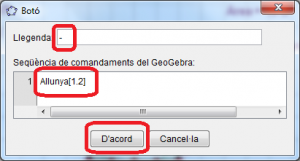
Figura 9

10.- Caselles de control

Les caselles de control són la forma visible de les variables booleanes, definireu 5 variables per a controlar la visualització de tots els objectes. Aquesta possibilitat permet minimitzar els elements visibles per a realitzar les diferents activitats.

Noms = true

Teorema = true

Angles = true

Superfície = true

Diagonals = true

Visualitzeu-los, i ordeneu-los en la finestra gràfica, també podeu modificar el color (Figura 10).

Ara és el moment de determinar la visibilitat de tots els objectes en la finestra de preferències en la solapa “Avançat” en l’opció “Condició per mostrar l’objecte. La llista és la següent

Objecte Condició per mostrar l’objecte

TextNom Noms

TextConcavitat QuadrilàterSimple ∧ Noms

TextTeoremaPick QuadrilàterSimple ∧ Teorema

TextÀrea QuadrilàterSimple ∧ Superfície

α QuadrilàterSimple ∧ Angles

β QuadrilàterSimple ∧ Angles

γ QuadrilàterSimple ∧ Angles

δ QuadrilàterSimple ∧ Angles

d_1 QuadrilàterSimple ∧ Diagonals

d_2 QuadrilàterSimple ∧ Diagonals

PuntsInteriors QuadrilàterSimple ∧ Teorema

PuntsVora QuadrilàterSimple ∧ Teorema

Q QuadrilàterSimple ∧ Superfície

Noms QuadrilàterSimple

Teorema QuadrilàterSimple

Superfície QuadrilàterSimple

Angles QuadrilàterSimple

Diagonals QuadrilàterSimple

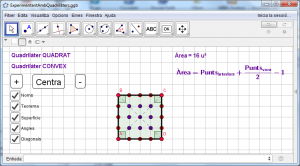
Figura 10

11.- Els colors dels costats, els angles i les diagonals

La idea consisteix a utilitzar el mateix color per a costats de la mateixa longitud, per a angles iguals i per a diagonals de la mateixa longitud i, en el cas de diagonals perpendiculars, les fareu més gruixudes.

GeoGebra permet utilitzar colors dinàmics, però s’han d’utilitzar tres instruccions per objecte i controlar fins a quatre colors, les instruccions condicionals poden arribar a ser extremadament complexes. Per això entrareu en el terreny del sistema de programació JavaScript inclòs en GeoGebra.

En la finestra “Preferències”, en la solapa “Seqüències de comandament” i en la següent solapa “JavaScript Global” observareu una funció que no utilitzareu, però no heu d’esborrar-la, function ggbOnInit() {}.

A continuació d’aquesta funció escriureu la funció colors() que explicaré amb comentaris. La doble barra indica que la resta del text de la línia és un comentari que podeu ometre. La funció fa lectura de les dades de GeoGebra a JavaScript i a continuació assigna els colors als objectes de GeoGebra. Teniu la relació de funcions de JavaScript per a treballar amb GeoGebra en la web (IGI 2016c, 2016d).

function colors(){

d1=ggbApplet.getValue(‘d_1’); // lectura de la longitud de la primera diagonal

d2=ggbApplet.getValue(‘d_2’); // lectura de la longitud de la segona diagonal

d=ggbApplet.getValue(‘DiagonalsPerpendiculars’); // lectura de la perpendicularitat

a1=ggbApplet.getValue(‘α’); // lectura del primer angle, les lletres greges les teniu que copiar i enganxar

a2=ggbApplet.getValue(‘β’); // lectura del segon angle

a3=ggbApplet.getValue(‘γ’); // lectura del tercer angle

a4=ggbApplet.getValue(‘δ’); // lectura del quart angle

s1=ggbApplet.getValue(‘a’); // lectura de la longitud del primer costat

s2=ggbApplet.getValue(‘b’); // lectura de la longitud del segon costat

s3=ggbApplet.getValue(‘c’); // lectura de la longitud del tercer costat

s4=ggbApplet.getValue(‘d’); // lectura de la longitud del quart costat

q=ggbApplet.getValue(‘QuadrilàterSimple’); // lectura de si és un quadrilàter simple

if (q==1) { // És un quadrilàter simple i calculem colors

ggbApplet.setColor(‘d_1’,0,0,255); // la primera diagonal és de color blau

if (d1==d2){ // les diagonals són iguals

ggbApplet.setColor(‘d_2’,0,0,255); // la segona diagonal també és de color blau

} else { // les diagonals no són iguals

ggbApplet.setColor(‘d_2’,255,0,255); // la segona diagonal és de color rosa

};

if (d==1){ // les diagonals són perpendiculars

ggbApplet.setLineThickness(‘d_1’,3); // la primera diagonal és grossa

ggbApplet.setLineThickness(‘d_2’,3); // la segona diagonal és grossa

} else { // les diagonals no són perpendiculars

ggbApplet.setLineThickness(‘d_1’,1); // la primera diagonal és fina

ggbApplet.setLineThickness(‘d_2’,1); // la segona diagonal és fina

};

ggbApplet.setColor(‘α’,255,127,0); // el primer angle és taronja

if (a2==a1) { // el segon angle és igual al primer

ggbApplet.setColor(‘β’,255,127,0); // el segon angle és taronja

} else { // el segon angle és diferent al primer

ggbApplet.setColor(‘β’,51,153,0); // el segon angle és verd

};

if (a3==a1) { // el tercer angle és igual al primer

ggbApplet.setColor(‘γ’,255,127,0); // el tercer angle és taronja

} else if (a3==a2) { // el tercer angle és igual al segon

ggbApplet.setColor(‘γ’,51,153,0); // el tercer angle és verd

} else { // el tercer angle és diferent del primer i del segon

ggbApplet.setColor(‘γ’,255,102,153); // el tercer angle és rosa

};

if (a4==a1) { // el quart angle és igual al primer

ggbApplet.setColor(‘δ’,255,127,0); // el quart angle és taronja

} else if (a4==a2) { // el quart angle és igual al segon

ggbApplet.setColor(‘δ’,51,153,0); // el segon angle és verd

} else if(a4==a3) { // el quart angle és igual al tercer

ggbApplet.setColor(‘δ’,255,102,153); // el quart angle és rosa

} else { // el quart angle és diferent del primer, del segon i del tercer

ggbApplet.setColor(‘δ’,102,153,255); // el quart angle és blau

};

ggbApplet.setColor(‘a’,255,127,0); // el primer costat és taronja

if (s2==s1) { // el segon costat és igual al primer

ggbApplet.setColor(‘b’,255,127,0); // el segon costat és taronja

} else { // el segon costat és diferent del primer

ggbApplet.setColor(‘b’,51,153,0); // el segon costat és verd

};

if (s3==s1) { // el tercer costat és igual al primer

ggbApplet.setColor(‘c’,255,127,0); // el tercer costat és taronja

} else if (s3==s2) { // el tercer costat és igual al segon

ggbApplet.setColor(‘c’,51,153,0); // el tercer costat és verd

} else { // el tercer costat és diferent del primer i del segon

ggbApplet.setColor(‘c’,255,102,153); // el tercer costat és rosa

};

if (s4==s1) { // el quart costat és igual al primer

ggbApplet.setColor(‘d’,255,127,0); // el quart costat és taronja

} else if (s4==s2) { // el quart costat és igual al segon

ggbApplet.setColor(‘d’,51,153,0); // el quart costat és verd

} else if(s4==s3) { // el quart costat és igual al tercer

ggbApplet.setColor(‘d’,255,102,153); // el quart costat és rosa

} else { // el quart costat és diferent del primer, del segon i del tercer

ggbApplet.setColor(‘d’,102,153,255); // el quart costat és blau

};

ggbApplet.setColor(‘A’,255,0,0); // els quatre vèrtexs són rojos

ggbApplet.setColor(‘B’,255,0,0);

ggbApplet.setColor(‘C’,255,0,0);

ggbApplet.setColor(‘D’,255,0,0);

} else { // no és un quadrilàter simple i tot és de color negre

ggbApplet.setColor(‘a’,0,0,0);

ggbApplet.setColor(‘b’,0,0,0);

ggbApplet.setColor(‘c’,0,0,0);

ggbApplet.setColor(‘d’,0,0,0);

ggbApplet.setColor(‘A’,0,0,0);

ggbApplet.setColor(‘B’,0,0,0);

ggbApplet.setColor(‘C’,0,0,0);

ggbApplet.setColor(‘D’,0,0,0);

};

}

Ara cal activar la funció cada vegada que menegeu un vèrtex, però hi ha un problema. Pot ocórrer que un objecte de GeoGebra execute la funció de JavaScript abans d’actualitzar la resta d’objectes, des de JavaScript seria impossible conèixer el valor actual de les variables de GeoGebra, per tant no podeu utilitzar el moviment dels punts per a connectar JavaScript amb GeoGebra.

Utilitzareu una variable que garantisca que tots els valors dels objectes de GeoGebra que han de ser transferits a JavaScript es calculen abans d’executar la funció.

dades = ” ” + α + ” ” + β + ” ” + γ + ” ” + δ + “” + a + ” ” + b + ” ” + c + ” ” + d + ” ” + QuadrilàterSimple

Per a poder concatenar els valors dels nou objectes, primer s’han de calcular, i ara sí que podeu executar la funció de JavaScript cada vegada que es modifique aquest text.

En la finestra de preferències (Figura 11), activeu el text “dades” i en la solapa “Bàsic” desactiveu l’opció “Mostra objecte”; en la solapa “Seqüències de comandament” cliqueu la solapa “En actualitzar” i escriviu la sentència

colors();

Seleccioneu l’opció JavaScript abans de clicar el botó “D’acord”

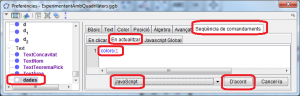
Figura 11

12.- Les capes

Els punts dels encreuaments estan per sota dels costats i les diagonals, i també heu de garantir que els vèrtexs estan per damunt de qualsevol altre objecte per a poder seleccionar-los sense cap dificultat.

A la finestra de preferències, seleccioneu les llistes “PuntsInteriors” i “PuntsVora” i en las solapa “Avançat” seleccioneu la capa 1.

Ara seleccioneu els quatre vèrtexs i en la solapa “Avançat” seleccioneu la capa 2.

Verifiqueu i guardeu el treball.

Referències Bibliogràfiques

Couchoud, J. M. (2016). Quadrilàters i el teorema de Pick. Recuperat de https://www.geogebra.org/m/pdW4wQCj

IGI (2016a). GeoGebra 5.0 Manual. International GeoGebra Institute. Recuperat de https://www.geogebra.org/manual/en/Manual

IGI (2016b). Manual de GeoGebra 5.0. International GeoGebra Institute. Recuperat de https://www.geogebra.org/manual/es/Manual

IGI (2016c). Reference:JavaScript. International GeoGebra Institute. Recuperat de https://www.geogebra.org/manual/en/Reference:JavaScript

IGInstitute (2016d), Referencia: JavaScript. International GeoGebra Institute. Recuperat de https://www.geogebra.org/manual/es/Referencia:JavaScript

MECE (2015). Ordre ECD/65/2015, de 21 de gener, per la qual es descriuen les relacions entre les competències, els continguts i els criteris d’avaluació de l’educació primària, l’educació secundària obligatòria i el batxillerat. BOE, suplement en llengua catalana al núm. 25, secc. I, pàg. 1. Recuperat de https://www.boe.es/boe_catalan/dias/2015/01/29/pdfs/BOE-A-2015-738-C.pdf

Motormuis (2014). Formule van Georg Pick. Recuperat de https://www.geogebra.org/m/DdUgCYn6

Juan Manuel Couchoud Pérez
Professor de matemàtiques
IES Vall de la Safor de Vilallonga
juan.manuel.couchou@gmail.com
https://www.geogebra.org/couchoud
@JuanmaCouchoud

GeoGebra₍₅₎ geometria₍₁₎ interactiva₍₁₎ Pick₍₁₎ quadrilàters₍₁₎